
Université des sciences et de la technologie Houari Boumediene.
Institut de génie mécanique
Thème

Élaboré par :
KHIAT
ALI.SEFIANE BADREDDINE.
1. Historique
:Au siècle dernier, Charles Darwin observa les phénomènes naturels et fit les constatations suivantes :
- l'évolution n'agit pas directement sur les êtres vivants ; elle opère en réalité sur les chromosomes contenus dans leur ADN.
- l'évolution a deux composantes : la sélection et la reproduction.
- la sélection garantit une reproduction plus fréquente des chromosomes les plus forts.
- la reproduction est la phase durant laquelle s'effectue l'évolution.
Dans les années 60s, John H. Holland expliqua comment ajouter de l'intelligence dans un programme informatique avec les croisements (échangeant le matériel génétique) et la mutation (source de la diversité génétique).
Il formalisa ensuite les principes fondamentaux des algorithmes génétiques :
- la capacité de représentations élémentaires, comme les chaînes de bits, à coder des structures complexes.
- le pouvoir de transformations élémentaires à améliorer de telles structures.
Et récemment, David E. Goldberg ajouta à la théorie des algorithmes génétiques les idées suivantes :
- un individu est lié à un environnement par son code d'ADN.
- une solution est liée à un problème par son indice de qualité.
2. Terminologie :
Les applications des AG sont multiples : optimisation de fonctions numériques difficiles (discontinues…), traitement d’image (alignement de photos satellites, reconnaissance de suspects…), optimisation d’emplois du temps, optimisation de design, contrôle de systèmes industriels [Beasley, 1993a], apprentissage des réseaux de neurones [Renders, 1995], etc.
Les AG peuvent être utilisés pour contrôler un système évoluant dans le temps (chaîne de production, centrale nucléaire…) car la population peut s’adapter à des conditions changeantes. Ils peuvent aussi servir à déterminer la configuration d’énergie minimale d’une molécule.
Les AG sont également utilisés pour optimiser des réseaux (câbles, fibres optiques, mais aussi eau, gaz…), des antennes [Reineix, 1997]… Ils peuvent être utilisés pour trouver les paramètres d’un modèle petit-signal à partir des mesures expérimentales [Menozzi, 1997]
4. Principe
: pour utiliser les techniques génétiques il faut faire deux opérations :1-Une fonction de codage de données en entrée sous forme d’une séquence de bits.
2-Trouver une fonction U(x) pour pouvoir calculer l’adaptation d’une séquence de bits x.
Après trouver ces deux fonctions on peut appliquer l’AG :
1- Générer aléatoirement quelques séquences de bits pour composer la
soupe initiale.
2- Mesurer l’adaptation de chacune des séquences présentes.
3- Reproduction des séquences en fonction de son adaptation.
4- Faire l’opération de croisement aléatoirement de quelque paire de séquences, et ce sera :
- une séquence est composée de la 1ere partie de la 1ere séquence et de la 2nd partie de la 2nd séquence.
- et une séquence est composée de la 2nd partie de la 1ere séquence et de la 1ere partie de la 2nd séquence.
5- Faire l’opération de mutation d’un bit choisi aléatoirement dans une ou
plusieurs séquences.
6- Retour à l’étape 2 (mesurer l’adaptation à nouveau).
II- les opérateurs :
1 - Codage binaire et réel des variables :
Pour résoudre un problème il faut d’abord coder les paramètres, un gène Correspond à une variable d’optimisation Xi, et un ensemble de gène correspond à un chromosomes un individu a un ou plusieurs chromosomes et une population c’est un ensemble des individus.
Dans l’informatique nous utilisons un codage binaire (0 et 1), par exemple un gène est un entier long (32 bits ).
Les cinq niveaux d’organisation schéma du codage de variable d’optimisation Xi de notre AG
Un des avantages du codage binaire est que l’on peut facilement coder les objets : réels, des entiers, des chaînes de caractères …etc.
Pour résoudre il nous faut un espace de recherche fini :
0 ‹ gi ‹ gmax i =1 a n
avec :gmax = 2**32 –1=4294967295 valeurs discrètes.
Chaque gène est codé par 32 bits.
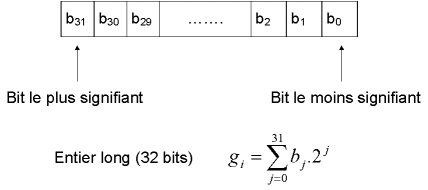
Les formules de codage et de décodage sont :
gi =( xi-ximin / ximax-xmin ) gmax.
xi= ximin + ( ximax-ximin )gi / gmax
Contrairement au codage binaire, dans le codage réel il n’y a pas d’opération de conversion vers le réel et le binaire, et alors l’AG soit plus dépendant du problème, chacune des composantes correspond à une inconnue du problème. Et pour l’insertion des chromosomes soit :
- Par l’insertion des chromosomes directement dans la population de la génération suivante.
2 - Sélection :
Représentation schématique du fonctionnement de l’AG
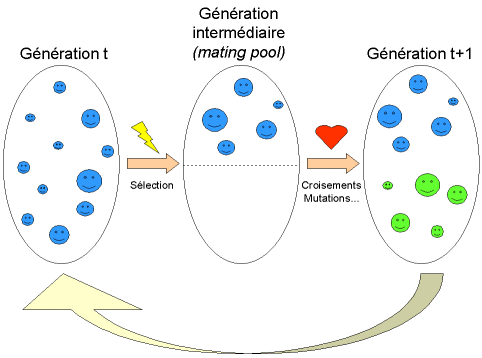
Il y’ a plusieurs méthodes de sélection, citons quelques-unes :
a/ Roulette de casino : C’est la sélection naturelle la plus employée pour l’AG binaire. Chaque chromosome occupe un secteur de roulette dont l’angle est proportionnel à son indice de qualité. Un chromosome est considéré comme bon aura un indice de qualité élevé, un large secteur de roulette et alors il aura plus de chance d’être sélectionné.
B/ " N/2 –élitisme " : Les individus sont tries selon leur fonction d’adaptation, seul la moitié supérieure de la population correspondant aux meilleurs composants est sélectionnée, nous avons constates que la pression de sélection est trop forte, il est important de maintenir une diversité de gènes pour les utilise dans la population suivante et avoir des populations nouvelles quant on les combine.
C/ "par tournoi " : Choisir aléatoirement deux individus et on compare leur fonction d’adaptation (combattre) et on accepte la plus adapte pour accéder à la génération intermédiaire, et on répète cette opération jusqu'à remplir la génération intermédiaire (N/2 composants). Les individus qui gagnent à chaque fois on peut les copier plusieurs fois ce qui favorisera la pérennité de leurs gènes.
3 - Croisement :
Le phénomène de croisement est une propriété naturelle de l’ADN, et c’est analogiquement qu’on fait les opérations de croisement dans les AG.
a / croisement binaire :
a-1 / " croisement en un point " : on choisit au hasard un point de croisement, pour chaque couple (fig. 1). Notons que le croisement s’effectue directement au niveau binaire, et non pas au niveau des gènes. Un chromosome peut donc être coupé au milieu d’un gène.
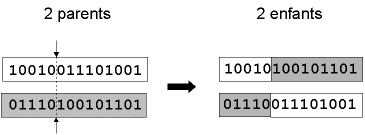
Fig. 1 : représentation schématique du croisement en 1 point. Les chromosomes sont bien sûr généralement beaucoup plus longs.
a-2 / " croisement en deux points " : On choisit au hasard deux points de croisement (Fig. 2). Par la suite, nous avons utilisé cet opérateur car il est généralement considéré comme plus efficace que le précédent [Beasley, 1993b]. Néanmoins nous n’avons pas constaté de différence notable dans la convergence de l’algorithme.
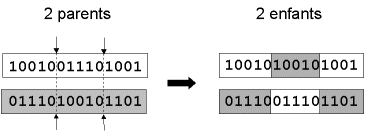
Fig. 2 : représentation schématique du croisement en 2 points.
Notons que d’autres formes de croisement existent, du croisement en k points jusqu’au cas limite du croisement uniforme.
b / Croisement réel :
Le croisement réel ne se différencie du croisement binaire que par la nature des éléments qu'il altère : ce ne sont plus des bits qui sont échangés à droite du point de croisement, mais des variables réelles.
c / Croisement arithmétique :
Le croisement arithmétique est propre à la représentation réelle. Il s'applique à une paire de chromosomes et se résume à une moyenne pondérée des variables des deux parents.
Soient [ai, bi, ci] et [aj, bj, cj] deux parents, et p un poids appartenant à l'intervalle [0, 1],
alors les enfants sont [pai + (1-p)aj, pbi + (1-p)bj, pci + (1 - p)cj] ...
Si nous considérons que p est un pourcentage, et que i et j sont nos deux parents, alors l'enfant i est constitué à p% du parent i et à (100-p)% du parent j, et réciproquement pour l'enfant j.
4 - Mutation :
Nous définissons une mutation comme étant l’inversion d’un bit dans un chromosome (Fig. 3 ). Cela revient à modifier aléatoirement la valeur d’un paramètre du dispositif. Les mutations jouent le rôle de bruit et empêchent l’évolution de se figer. Elles permettent d’assurer une recherche aussi bien globale que locale, selon le poids et le nombre des bits mutés. De plus, elles garantissent mathématiquement que l’optimum global peut être atteint.
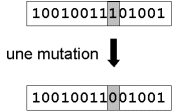
Fig. 3 : représentation schématique d’une mutation dans un chromosome.
D’autre part, une population trop petite peut s’homogénéiser à cause des erreurs stochastiques : les gènes favorisés par le hasard peuvent se répandre au détriment des autres. Cet autre mécanisme de l’évolution, qui existe même en l’absence de sélection, est connu sous le nom de dérive génétique. Du point de vue du dispositif, cela signifie que l’on risque alors d’aboutir à des dispositifs qui ne seront pas forcément optimaux. Les mutations permettent de contrebalancer cet effet en introduisant constamment de nouveaux gènes dans la population [Beasley, 1993b].
Comment réaliser notre opérateur mutation ? De nombreuses méthodes existent. Souvent la probabilité de mutation pm par bit et par génération est fixée entre 0,001 et 0,01. On peut prendre également pm=1/l où l est le nombre de bits composant un chromosome. Il est possible d’associer une probabilité différente de chaque gène. Et ces probabilités peuvent être fixes ou évoluer dans le temps.
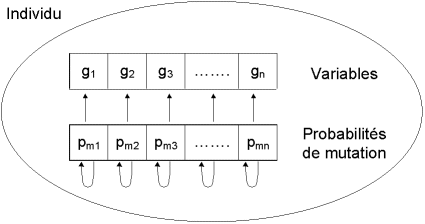
Fig. 4 : principe de l’auto-adaptation. A chaque variable est associée sa propre probabilité de mutation, qui est elle-même soumise au processus d’évolution. L’individu possède donc un second chromosome codant ces probabilités.
Après divers essais, ils ont abouti à la méthode d’auto-adaptation des probabilités de mutation [Bäck, 1992]. Si dans un environnement stable il est préférable d’avoir un taux de mutation faible, la survie d’une espèce dans un environnement subissant une évolution rapide nécessite un taux de mutation élevé permettant une adaptation rapide. Les taux de mutation d’une espèce dépendent donc de leur environnement [Wills, 1991].
Pour prendre en compte cette formulation biologique et l’adapter à notre cas, ils ont introduit dans chaque individu (dispositif) un second chromosome (ensemble de paramètres) dont les gènes (paramètres) représentent les probabilités de mutation de chaque gène du premier chromosome (Fig. 4 ). Ce second chromosome est géré de façon identique au premier, c’est-à-dire qu’il est lui-même soumis aux opérateurs génétiques (croisement et mutation). Cela revient à fixer les probabilités assurant la modification des valeurs des paramètres du composant en fonction des valeurs d’un ensemble d’autres paramètres (les probabilités de mutation).
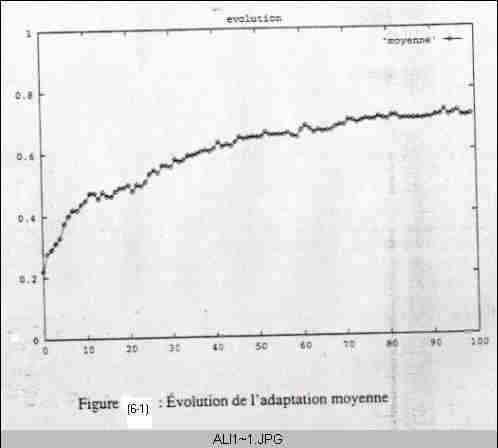
Lors de la genèse, les probabilités de mutation sont posées égales à 0,1 (valeur qui a paru la meilleure après plusieurs essais). Au cours du déroulement de l’algorithme, les gènes et les individus ayant des probabilités de mutation trop élevées ont tendance à disparaître. De même, les gènes ayant des probabilités de mutation trop faibles ne peuvent pas évoluer favorablement et tendent à être supplantés. Les probabilités de mutation dépendent donc du gène considéré et de la taille de la population. De plus, elles évoluent au cours du temps. Il y a donc auto-adaptation des probabilités de mutation.
a / Mutation binaire :
La mutation binaire s'applique à un seul chromosome. Un bit du chromosome est tiré au hasard. Sa valeur est alors inversée.
Il existe une variante où plusieurs bits peuvent muter au sein d'un même chromosome. Un test sous le taux de mutation est effectué non plus pour le chromosome mais pour chacun de ses bits : en cas de succès, un nouveau bit tiré au hasard remplace l'ancien.
b / mutation réelle :
La mutation réelle ne se différencie de la mutation binaire que par la nature de l'élément qu'elle altère : ce n'est plus un bit qui est inversé, mais une variable réelle qui est de nouveau tirée au hasard sur son intervalle de définition.
c / mutation non uniforme :
La mutation non uniforme possède la particularité de retirer les éléments qu'elle altère dans un intervalle de définition variable et de plus en plus petit. Plus nous avançons dans les générations, moins la mutation n'écarte les éléments de la zone de convergence. Cette mutation adaptative offre un bon équilibre entre l'exploration du domaine de recherche et un affinement des individus.
Le coefficient d'atténuation de l'intervalle est un paramètre de cet opérateur.
III - Exemples d’application des AG :
1- Exemple(1) :
Principe :
Applique l’AG sur l’optimisation de la trajectoire d’avion dans le plan horizontal, avec les hypothèses suivantes :
- A chaque avion un point de départ et un point d’arrivée.
- Les deux avions volent à une vitesse constante.
- la distance entre avion ne doit pas être au-dessous de 15Km.
- Si les deux avions volent en ligne droite ils entreront en conflit.
- Les deux avions peuvent seulement change de cape.
Modélisation du problème :
- Les deux avions sont considérés comme des points matériels qui se déplacent à une vitesse constante égale par exemple a 220m/s.
- L’avion peut manœuvrer de trois façons : virer soit à droite, soit à gauche d’un angle donné (30°), nous n’appliquons pas la montée et la descente car au contrôle aérien ces deux manœuvres sont utilise qu’au dernier recoure à cause de leur coût de consommation et de confort du passager.
- Nous prenons le pas de discrétisation de 16 (Le temps devise en intervalle de longueur fixe)
Application de l’AG :
La première opération c’est le codage :
Nous codons les trois mouvements possibles de l’avion sur deux bits :
- la ligne droite par 00 et 01.
- tourner à droite par 10.
- Tourner à gauche par 11.
Le critère d’évaluation retenu est la distance restante à parcourir pour rejoindre le point d’arrivée après l’application des 16 actions codées par la séquence (ceci équivalant strictement a mesurer la distance totale parcourue puisque la distance parcourue en un pas est constante ).
Il est ramené à l’intervalle [0,1] la formule empirique suivante :A=e**(-(d/2ds)²)……(ks)
Ou : d : la distance restante à parcourir.
ds : la distance de séparation (15km).
Les séquences de trajectoire ne respectent pas la norme de sécurité sont affectées d’une adaptation nulle.
La difficulté de cette méthode est de définir une bonne fonction d’adaptation ainsi que de régler les différents paramètres régissants l’évolution des séquences.
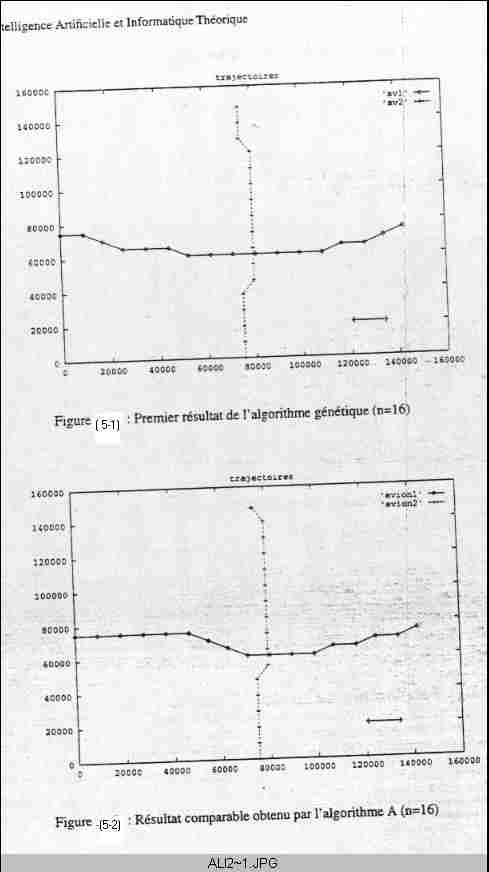
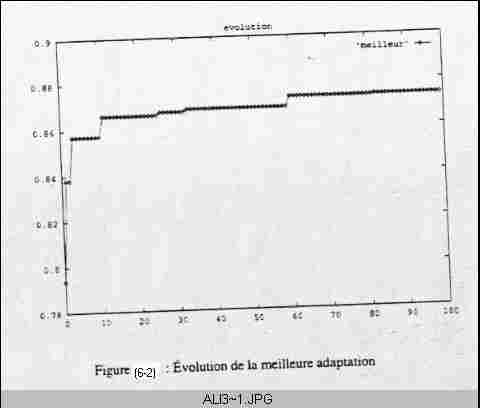
La figure 5.1 montre une solution obtenue après 54 générations de l’AG.
Les paramètres choisis étaient :
- population comprenant 400 individus.
- 60% de croisement à chaque génération.
- 0.1% de mutation à chaque génération.
Cette solution est optimale, après l’application de l’algorithme (ks) on obtient des résultats équivalents à celle de l’AG mais dans un temps très long.
Amélioration du modèle :
Principe :
Modélisation :
Modification de la fonction d’adaptation :
A=e**(-0.04[((d/dm)**4)+(c/cmin)²])
Ou :
2- Exemple (2) :
la recherche du maximum d'une fonction du type y=f(x).
Un algorithme génétique travaille à partir d'un ensemble d'éléments choisis au hasard dans un espace de solutions potentielles. Dans notre cas, l'ensemble de départ se composera de nombres tirés au hasard dans l'intervalle où nous recherchons le maximum.
Sa connaissance du problème à résoudre se résume à une fonction d'évaluation qui mesure la qualité d'un élément en tant que solution au problème. La fonction d'évaluation sera ici la fonction elle-même : le x donnant le plus grand y par f sera considéré comme le maximum de f dans l'ensemble de départ, appelé génération 1.
La qualité de ce maximum est bien entendue très médiocre puisqu'il a été choisi au hasard. Cependant, l'algorithme génétique va tirer parti des meilleurs éléments à sa disposition pour fabriquer de toutes pièces un nouvel ensemble d'éléments répondant en moyenne de mieux en mieux au problème.
Pour passer de l'ancien au nouvel ensemble, les éléments sont sélectionnés aléatoirement et proportionnellement à leur qualité en tant que solution au problème. Ainsi, le x que nous avons considéré comme maximum aura plus de chances d'être sélectionné que les autres éléments. S’il est retenu, il contribuera à améliorer les éléments du nouvel ensemble. Dans le cas contraire, il est irrémédiablement perdu pour les ensembles futurs.
Les éléments sélectionnés sont ensuite combinés en de nouveaux éléments grâce à des méthodes inspirées de phénomènes naturels, comme le croisement génétique ou la mutation. Les méthodes seront détaillées dans les chapitres suivants. Il suffit d'admettre, pour l'instant, que nous obtenons un nouvel ensemble de x auxquels nous appliquerons f pour déterminer le maximum de la génération 2.
L'algorithme génétique travaille ensuite par générations successives jusqu'à un critère d'arrêt :
IV- Programmation génétique :
1- Idée principale :
Comment un ordinateur peut-il apprendre à résoudre un problème sans l'avoir explicitement programmé pour résoudre celui-ci ?
Beaucoup de problèmes en intelligence artificielle peuvent être résolus par la découverte d'un programme qui va fournir les sorties désirées sous l'impulsion d'entrées particulières. C'est ce que nous nous proposons de faire avec la programmation génétique.
La programmation génétique repose sur les algorithmes génétiques qu'on a dotés de structures plus complexes pour la représentation des chromosomes, ces structures étant des programmes.
2 - Représentation des programmes :
Ces programmes, suivant le problème à traiter, peuvent être la traduction d'une fonction arithmétique, d'une fonction logique, d'un chemin à suivre pour atteindre une cible... On pourra les représenter par des S-expressions à la LISP ou encore sous forme d'arbre :
1- Exemple : La fonction ((a+b)*c) se traduit par :
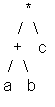
3- Mécanismes :
comme pour les algorithmes génétiques, on part d'un ensemble de programmes choisis au hasard parmi tous les programmes possibles de l'espace des solutions. La qualité de chaque programme est obtenue à l'aide d'une fonction d'évaluation. Puis on va élaborer le meilleur programme possible au cours des différentes générations grâce à la reproduction et aux opérateurs de croisement et de mutation génétique. Ainsi, "l'ordinateur" va trouver un programme permettant de répondre le plus précisément possible à un critère traduit par la fonction d'évaluation à partir d'un ensemble d'opérateurs pouvant constituer le programme.
Exemple: Soit une fourmi qui cherche à manger un nombre maximum d'aliments, ceux-ci étant disposés dans l'espace accessible par la fourmi. Le paramètre à évaluer est le nombre d'aliment effectivement mangé par la fourmi sachant que celle-ci peut :
a. Avancer
Le programme, résultant de la programmation génétique, nous permettra de connaître le meilleur chemin emprunté par la fourmi pour manger tous les aliments à partir de sa position initiale.
4. Opérateurs génétiques :
Les opérateurs génétiques utilisés pour la programmation génétique sont les mêmes que pour les algorithmes génétiques. Cependant, leur mise en œuvre peut s'avérer plus difficile du fait des données qu'ils manipulent.
Le croisement :
Pour effectuer le croisement entre deux chromosomes, qui sont des programmes, on va choisir au hasard un nœud de l'arbre dans chacun des programmes et on va échanger les sous-arbres obtenus à partir de chacun de ces nœuds d'un arbre à l'autre.
On obtient ainsi deux nouveaux chromosomes, soit deux nouveaux programmes.
Exemple:
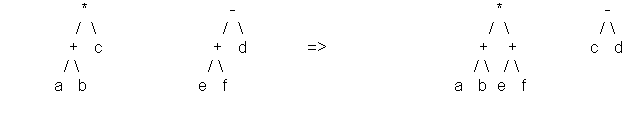
La mutation :
Pour effectuer une mutation sur un chromosome, qui est un programme, on va choisir au hasard un nœud de l'arbre et on va remplacer le sous-arbre partant de ce nœud par un nouveau sous-arbre généré au hasard. On obtient ainsi un nouveau chromosome, soit un nouveau programme.
Exemple:
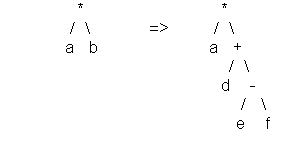
Ainsi, la programmation génétique permet de résoudre un très grand nombre de problèmes et d'obtenir des solutions complexes sous forme de programmes. Les problèmes résolubles par cette méthode, sont tous les problèmes où interviennent un nombre fini d'opérations que l'on peut mettre sous la forme d'un programme et où l'on peut trouver une fonction d'évaluation.
V- Les problèmes de l’algorithme génétique :
1- le codage :
L’un des problèmes les plus importants est le codage des données :
2- La dominance :
La domination d’un chromosome provoque la disparition rapide de certains élément de la population, mais la méthode des AG présente plusieurs solutions contrairement a d’autres algorithmes comme recuit simulé qui présent une seule solution, alors il faut éliminer les chromosomes et laisser le meilleur (le mieux adapté).
3- Le croisement :
L’un des problèmes des AG c’est la position de codage, par exemple : une propriété importante est codée dans une chaîne de 8 bits par le 1er et le 8th bit, dans ce cas tout croisement peut ce faire facilement mais si le codage est fait entre le 1er et le 2nd bit le croisement sera presque insensible.
C’est de ca ou vient l’idée de réorganisé les bits dans un chromosome de façon à crée des blocs stables.
4-Les chromosomes haploïdes et diploïdes :
Un chromosome haploïde a une chaîne de bits et un chromosome diploïde a deux chaînes de bits.
Un chromosome haploïde est beaucoup utilise par rapport au chromosome diploïde, ce dernier n’est efficace que lorsque la fonction de fitness varie en fonction du nombre de génération de l’AG f(c, n) (ou n est le numéro de génération de l’A.G.) au lieu d’être simplement en fonction de c.
Mais les organismes vivants les plus évolués ont des chromosomes diploïdes.
Les chromosomes diploïdes ont des grandes capacités a mémoriser par l’intermédiaire de gènes récessifs.
VI- AG et réseaux de neurones :
Entre l’AG et les réseaux de neurones une intéressante combinaison comme le montre l’exemple suivant :
Nous considérons 6 mobiles a chacun un point de départ et un point d’arrivée, nous voulons qu’ils atteignent leurs points finals sans dépasser une distance D entre eux, avec le chemin le plus court.
Pour résoudre le problème on construit un réseau de neurone, qui relient les différentes donnes pour rejoindre l’arrivée, comme il n’existe pas une solution mathématique de ce problème, c.a.d de réalise un apprentissage du réseau, on peut utiliser l’AG pour calculer les poids du réseau de neurones, commençant par générer un certain poids en suite on déplace les mobiles en plusieurs exemples, on trouve plusieurs adaptations des chromosomes, c’est les trajectoires générées, et le chemin optimal c’est le plus court avec l’évitement entre eux, et toutes les trajectoires qui ne respectent pas les conditions seront soit annuler soit diviser par un coefficient donné. On tire aléatoirement deux coefficients dans deux réseaux est on fait leur croisement pour obtenir les nouveaux coefficients, est pour la mutation on ajoute un bruit blanc sur un coefficient aléatoirement et en suite on obtient un réseau et on cherche la fitness à nouveau.
VII- Conclusion :
Les algorithmes génétiques peuvent être utilisés en tant que méthode de recherche combinatoire incluant, des propriétés base sur le parallélisme et l’exploration, des heuristiques de recherche intéressante basées sur des principes d’auto-organisation.
Les algorithmes génétiques peuvent constituer une alternative intéressante lorsque les méthodes d’optimisation traditionnelles (méthode "grimpeur ", méthodes analytiques telle que les moindres-carrés) ne parviennent pas à fournir efficacement des résultats fiables.
Cependant, comme nous l’avons souvent souligne au cours de ce mini-projet, la plupart des mises en œuvre courantes des AG nécessitent un environnement (le processus ou un modèle de processus) suffisamment tolérant pour laisser à l’algorithme le "droit a l’erreur "
Ceci implique que l’environnement doit permettre l’essai et l’évaluation de solutions-condidates médiocres.
L’algorithme génétique employé seul constitue un mécanisme de recherche souvent "trop aveugle " alors il peut rendu plus efficace si on le combine avec des méthodes de recherche traditionnelles, habituellement plus locales (régulateur classique, régulateur flou ou un système de commande neuronal ).
Bibliographie :