

I -
Introduction.
II -
Théorie des ensembles Floues.
III -
Principe fondamental de la logique Floue.
IV -
Variables linguistiques.
V - Valeurs et variables linguistiques et fonction d’appartenance.
VI -
Déduction Floue (ou inférences).
VII -
Opérateur de la logique Floue.
VIII - Quelques domaines d’applications avec des exemples
I) Introduction :
Aujourd’hui, la logique Floue (en anglais Fuzzy logic) est de grande actualité.
L’opinion commette est qu’il s’agit d’une nouvelle méthode de traitement pour les problèmes de réglage et de prise de décision parvenant du JAPON. Ce pendant, cette augmentation n’est pas du tout correcte.
En effet, les bases théoriques de la logique floue ont été établies en 1995 par le professeur LOTFIA Zadeh de l’université de Californie de Berkeley. A cette époque, la théorie de la logique floue n’a pas été prise au sérieux. En effet, les ordinateurs avec leur fonctionnement exact par tout ou rien (1 et 0) ont commencé à se répondre sur large échelle. Par, contre la logique floue permet de traiter des variables non exactes dont la valeur peut varier entre net 0. Initialement, cette théorie a été appliquée dans des domaines non techniques, comme le commerce, les jurys-prudence ou la médecine, dans le but de compléter les systèmes experts, et afin de leur donner l’aptitude de prise de décision.
Dés 1975, on trouve les premières applications au niveau des systèmes de réglage. A partir de 1985 environ, ce sont les Japonais qui commencent à utiliser la logique floue dans des produits industriels pour résoudre des problèmes de réglage et de commande.
Tout récemment, aussi en Europe, une intense activité de recherche a débuté afin d’introduire le principe du réglage par logique floue.
I) Théorie des ensembles flous :
Un ensemble classique est un ensemble ayant une limite stricte ; prenons un exemple, A = {x / u > 5}.
Le point u = 5 est une limite claire, non ambiguë.
Si u est plus grand que 5, il appartient à A.
Un ensemble floue, est un ensemble sans limite stricte, la notion d’appartenance à un ensemble est graduelle, c’est à dire qu’un élément peut appartenir, plus au moins fortement à cet ensemble.
III) Principe fondamental de la logique floue :
Comparativement à la logique classique, les bases théoriques de la logique floue sont établies de manière à pouvoir traiter des variables inexactes de valeurs comprises entre 0 et 1, par contre la logique de Boole dont les variables ne peuvent prendre que les valeurs 0 et 1.
A titre d’exemple la classification des personnes à travers leur âge par les deux logiques présenté dans la figure (1).
Fait apparaître que :
Les limites ne varient pas soudainement, mais progressivement, la figure ( ) montre une classification possible ; une personne de 25 ans appartient à l’ensemble (jeune) avec une valeur u = 0.75 de la fonction d’appartenance, et à l’ensemble (entre deux âges) avec u = 0.25. par contre une personne de 70 ans appartient avec une valeur u = 1 de la fonction d’appartenance à l’ensemble (âge).
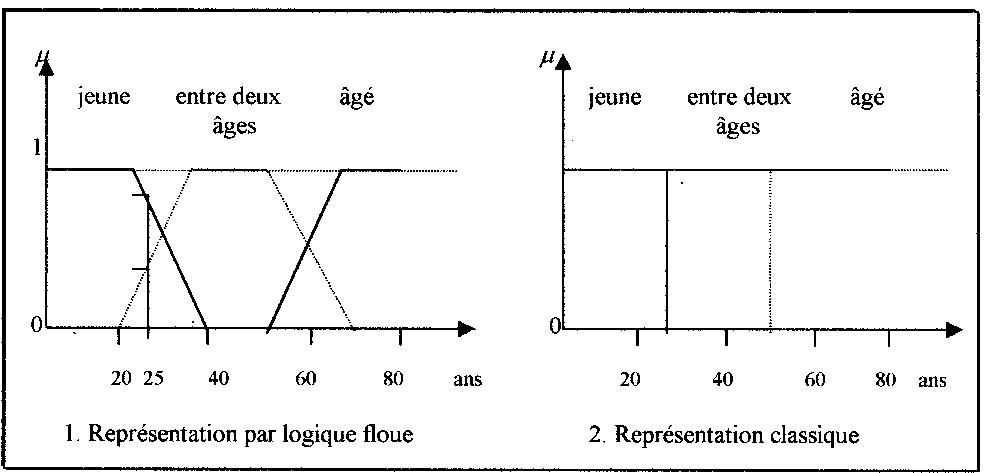
Figure (1)
IV) Variables linguistiques :
On désigne par variables linguistiques les termes utilisés lors de la description d’une situation, de phénomènes, on de procédés tels que : la température, l’âge, la vitesse, …etc.
L’expression de cette opération sera debout, accroupi, assis ou allongé pour décrire des positions ; pour la discrétion d’un procédé, elle sera formulée en général avec une succession de conditions suivies d’opérations tel que :
Si condition 1, alors opération 1, OU.
Si condition 2, alors opération 2, OU.
•
•
•
Si condition n, alors opération n, OU.
•
•
•
V)
Valeur des variables linguistiques et fonctionsd’appartenance :
Les valeurs des variables linguistiques sont la traduction linguistique que de divers états de ces dernières tel que : froid, tiède et chaud sont des valeurs de la variable linguistique température.
Ceci permet de décrire un processus sans avoir à faire à son traitement numérique.
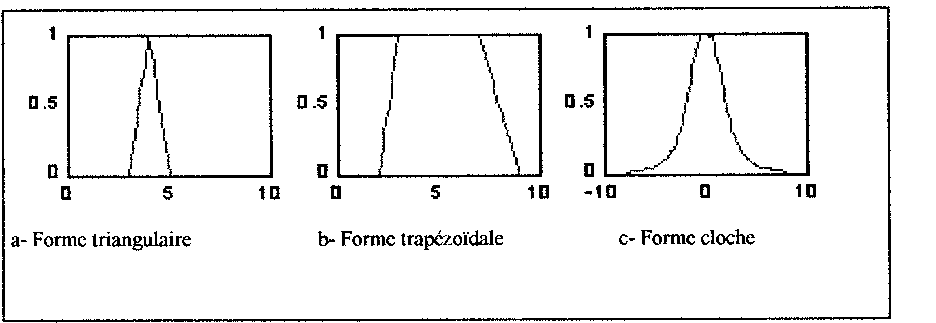
fig (2)
La description des valeurs des variables linguistiques par des fonctions mathématiques particulières fig (2), permet de définir leur domaine de prédominance (en tenant compte du processus) et de couvrir leur domaine de variation.
Exemple : On présente comme exemple le réglage de la T° d’un local dans le cas le plus simple, on peut distinguer deux valeurs " froid " et " très chaud " de la variable linguistique " température O ", elle forme deux ensembles floues
(fig 3.a), ainsi, une T° de 16° appartient avec un facteur d’appartenance µs e, 7 à l’ensemble " froid ", et avec µs 0,3 à l’ensemble " très chaud ".
Souvent, il s’avère nécessaire d’introduire une subdivision plus fine, par exemple avec quatre valeurs " froid ", " tiède ", " chaud " et " très chaud " pour la variable linguistique " température O " formant ainsi quatre ensembles comme le montre la (fig 3.b).
La T° de 16 appartient alors avec µs 0,1 à l’ensemble " froid ".Et avec µs 0,9 à l’ensemble " tiède ". Evidement, cette valeur de 16° n’appartient ni à l’ensemble " chaud " ni à celui " très chaud ".
VI) Déduction floues (ou inférences) :
En général, plusieurs valeurs des variables linguistiques convenablement définies par des fonctions d’appartenances, sont liées entre elles par des règles, afin de tirer des conclusions.
On parle alors de déduction floues ,ou inférences.
On peut distinguer deux types de règles d’inférences :
. inférence avec une seule règle.
. inférence avec plusieurs règles.
VI . 1) Inférence avec une seule règle :
Cette règle est appliquée dans des domaines non techniques lorsqu’il faut choisir un élément (qui représente l’optimum) parmi un ensemble.
Si x1,x2, ……. xn sont les variables linguistiques pour évaluer une certaine situation, le critère pour la prise de décision peut être formulé par une règle, comme par exemple :
Y=[ x1 ou (x2 et x3) ou ….] et xn.
A chaque variable formant un ensemble est attribué une fonction d’appartenance µx1, µx2, …….µxn.
Dont les valeurs numériques (facteurs d’appartenance) qui sont en générale différentes pour chaque élément I=1,2,……,n .
VI .2) Inférence avec plusieurs règles :
Dans ce cas présent, lorsqu’une ou plusieurs variables nécessitent une prise de décision différente suivant les valeurs qu’atteignent ces variables ; ces dernières sont des variables linguistiques donc des variables floues.
Cette problématique se présente essentiellement pour des problèmes de réglage et de commande, et la prise de décision conduit à l’exécution d’une certaine opération. Les règles peuvent alors être exprimées sous la forme générale.
Opération :
Si condition 1 alors opération 1ou
Si condition 2 alors opération 2 ou
.
.
Si condition n alors opération n.
VII) Opération de la logique floue :
Au niveau des inférences, les valables linguistiques sont liées entre elles par des opérations de la logique floue tel que et ou qui interviennent sur les fonctions d’appartenances représentant les variables linguistiques.
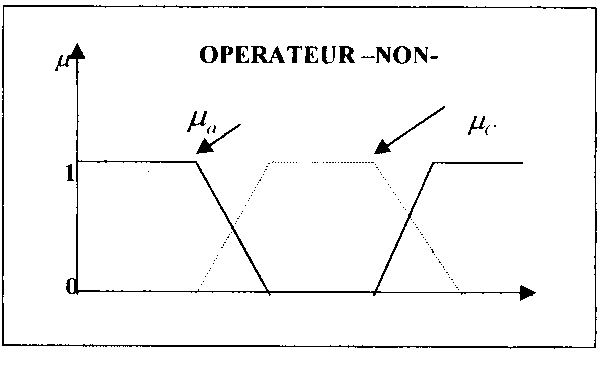
VII.1) Opération –Non- :
Le complément d’un ensemble floue A , dénoté par :
C = Ā (ou en anglais not A) est défini comme :
µc (x) = 1- µa (x) , que la figure (slide) met en évidence.
Figure (slide)
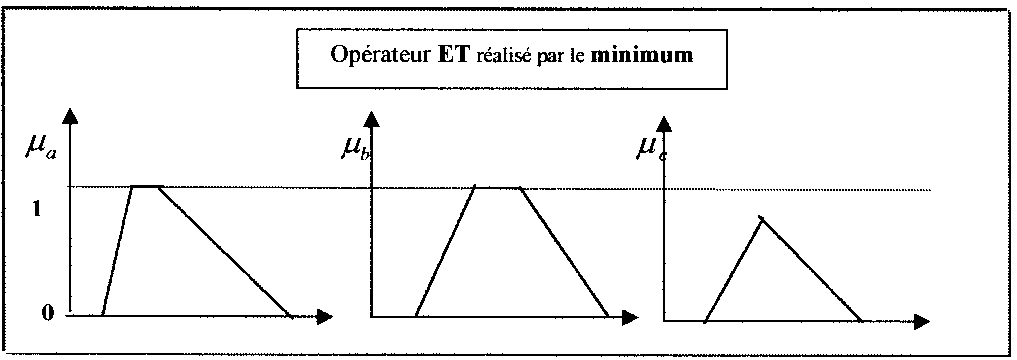
VII.2) Opération ET :
L’opération ET correspond à l’intersection de deux ensembles A et B , ou écrit : C = A ∩ B ou (A et B), l’opérateur ET de la logique floue est réalisé par la formulation du minimum , appliquée aux fonctions d’appartenances µa (x) et µb (x) des deux ensembles A ET B qui s’écrit par :
µc (x) = min [µa (n), µb (x) ]------------------(1)
· Le résultat de l’opération peut ne pas atteindre la valeur 1 comme le montre la figure ( ).
La commutativité et l’associativité restent valables même pour des variables différentes.
Figure (slide)
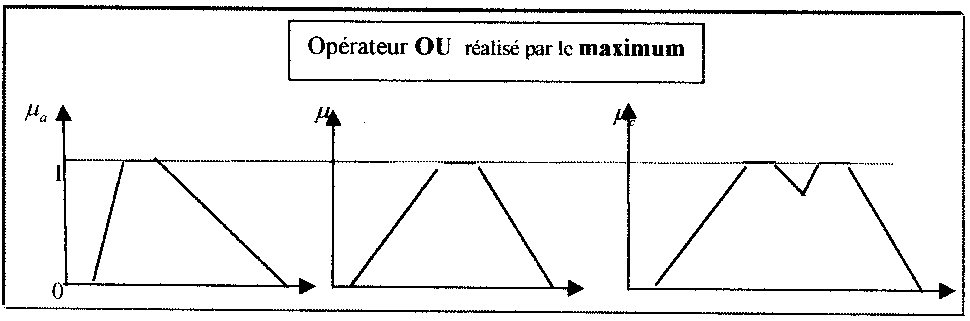
VII.3) Opérateur OU :
L’opération OU correspond à l’union de deux ensembles A et B , on écrit :
C = (AUB), ou (A ou B), la réalisation de l'opérateur Ou de la logique floue se fait par la formation du maximum, appliqué aux fonctions d’appartenance
µa (x) et µb (x) des deux ensembles A et B qui s’écrit par :
µc (x) = max [µa (x), µb (x)] --------(2)
Il est possible que la fonction d’appartenance µc (x) résultante atteigne deux fois la valeur 1. Comme le montre la figure ( ) . la commutativité et l’associativité restent valables même pour des variables différentes.
Figure (slide)
VIII) Autre réalisation pour les opérateurs ET et OU :
Il existe d’autres réalisation pour les opérateurs ET et OU qui sont moins utilisées pour le réglage et la commande par logique floue. Cependant, dans certaines circonstances, il peut être judicieux d’utiliser d’autres réalisations, soit pour simplifier le traitement numérique, soit pour mieux tenir compte des opérations floues.
VIII.1) Opérateurs ET réalisés par opérations arithmétiques :
• L’opération ET réalisée par opération arithmétique, obtenu par le produit des fonctions d’appartenances, et qui s’écrit :
µc (x) = µa (x) . µb (x) ---------------(3)-------------
• Par analogie l’opérateur OU réalisé par la moyenne de fonction d’appartenance, et qui s’écrit :
µc (x) = [ µa (x) + µb (x) ]-----------(4)------------
2
VIII.2) Opérateurs ET flou et OU flou :
Les opérateurs sont obtenus par combinaison entre l’opérateur minimum et l’opérateur maximum et la moyenne arithmétique.
• L’opérateur ET flou est défini par :
µc (x) = x min [µa (x), µb (x) ] + 1- x [µa (x) + µb (x) ]-----------(5)---------
2
• L’opération OU flou est défini par :
µc (x) = x max [µa (x), µb (x) ] + 1- x [µa (x) + µb (x) ]-----------(6)---------
2
avec : E [ 0,1] , il est possible de prendre l’influence des deux termes
( ET flou, OU flou).
Pour = 1 , on aboutit respectivement aux opérateurs min et max, et pour = 0, on aboutit à la moyenne arithmétique correspondante à l’opérateur somme.
Donc : le ET flou et le OU flou se confondent.
•
Opérateur min – max et opérateur :L’opérateur min – max est la combinaison des opérateurs minimum et maximum
Et qui s’écrit :
µc (x) = .min [µa (x), µb (x) ]+(1- ) . max [µa (x), µb (x) ]----------(7)----------
L’opérateur est défini par :
1- .
µc (x) = [µa (x) . µb (x) ] [ ( 1- [ 1- µa (x) ] [ 1- µb (x) ] ) ]----------(8)--------
1-
µc (x) = [µa (x) . µb (x) ] [µa (x) + µb (x) - µa (x) . µb (x) ]----------(9)-------
avec : E [ 0,1 ].
VIII) Quelques domaines d’application avec des
exemples :
VIII.1) La commande Floue :
Parmi les nombreuses applications de la logique floue, la commande floue s’avère être le champ d’application le plus actif à travers le monde.
Exemples :
VIII.2) Classification et reconnaissance de formes :
Classifier consiste à regrouper des objets en catégories les plus homogènes possibles (contenant des objets similaires) :
Classifier est une activité qui intervient dans des nombreux domaines d’applications tels que :