
U. S. T . H . B
Institut de génie mécanique


Introduction
![]()
![]()
![]()
![]()
![]() 0.4 - algorithmes génétiques parallèles et dynamique du population
0.4 - algorithmes génétiques parallèles et dynamique du population
Chapitre 1 (
Principe de fonctionnement)![]()
![]()
![]()
![]()
![]()
chapitre 2 (
codage binaire )![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
chapitre 3 (codage réel)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
chapitre 4 (
exemple explicatif )![]()
chapitre 5 (
conclusion générale )![]()
![]()
INTRODUCTION
D
éfinir ce qu’est l’intelligence est une question qu’il serait peu sage de soulever ; une réponse circonstanciée relève de l’utopie. Mais à défaut de cerner avec précision les concepts qui sous-tendent l’idée que chacun de nous se fait de l’intelligence, il est possible de réfléchir aux différentes formes que peut prendre l’intelligence.La première qui nous vient à l’esprit, le plus naturellement du monde, est l’intelligence humaine. La seconde, un peu moins immédiate, est l’intelligence collective, ou l’intelligence sociale. C’est une intelligence qui ne repose pas sur les facultés d’un seul individu comme le fait dans une certaine mesure l’intelligence humaine-mais sur l’interaction d’un grand nombre d’individus. Ce qui est remarquable, c’est qu’aucun des individus de cette fragile construction, s’il est pris séparément, ne saurait prétendre à une quelconque intelligence. Il ne nous viendrait pas à l’idée de dire qu’une fourmi ou une abeille est douée de raison. Et pourtant, il est manifeste qu’une fourmilière ou une ruche constitue une entité intelligente
La troisième forme d’intelligence, presque confidentielle même si elle subsumme en quelque sorte les deux autres est celle de l’évolution. Pour arriver à un homme capable de raisonner à une ruche dont les membres peuvent communiquer et coopérer, il fallu des millions d ‘années d’évolution. Or cette évolution n’est pas aveugle, en ce sens qu’elle a su utiliser le mécanisme le plus efficace pour préserver la vie : l’adaptation. En effet, arriver à trouver une solution à un problème aussi complexe que celui de la survie dans un environnement en perpétuelle mutation ne peut être dû uniquement au hasard. Certes, ladite solution n’est peut-être pas la plus optimale, mais elle est certainement satisfaisante.
C’est en cela que l’évolution des espèces est en soi une forme d’intelligence ; elle est peut
être la moins apparente, mais elle est une indubitablement la première à être apparue, une sorte d’intelligence originelle.
0.1- De l’évolution naturelle à l’évolution artificielle
Il est donc tout à fait naturel que des chercheurs d’horizons divers aient pensé à s’inspirer des mécanismes qui font la force du processus d’évolution. Tout a commencé avec la théorie de Darwin sur l’origine des espèces, et son célèbre principe du survival of the fittest, la survie des plus adaptés [Darwin,1859]. Mais ce qui n’était à l’origine qu’une théorie biologique est devenue entre les mains de pionniers comme [Hollond,1962] ou [Bagley,1967] un formidable outil d’optimisation, mêlant informatiques, mathématiques
Et biologique. [Holand,1975] pose les fondements théoriques des algorithmes, passant du
Paradigme de l’évolution naturelle à celui de l’évolution artificielle. L’idée qui préside à ce
Changement de perspective est à fois simple et élégante : puisque l’évolution semble être
un moyen efficace pour favoriser l’émergence de solutions adaptées à un environnement
complexe, pourquoi ne pas en simuler les processus pour trouver la solution globale à un problème donné? Pour résoudre le problème considéré, il suffit alors de générer une population de solutions potentielles qui évolueront dans l’ordinateur s’adapteront à l’environnement défini par le problème. Ces solutions sont représentées par l’équivalent digital d’un chromosome. Et c’est sur ce ADN digital que sont appliqués des opérateurs
qui s’inspirent tout naturellement des opérateurs classiques de la biologie, que ce soit le croisement, la mutation, ou la sélection.
0.2 - L’évolution artificielle, une méthode d’optimisation efficace
Une nouvelle étape est franchie lorsque les travaux de [Goldberg, 1989] donnent aux algorithmes génétiques leurs lettres de noblesse en tant que méthode d’optimisation viable, efficace, et non spécifique. Ils traduisent plus précisément les préoccupations d’un ingénieur
doublé d’un théoricien, tout aussi intéressé par des considérations purement théoriques que par les aspects applicatifs. Les quelques applications utilisant les algorithmes génétiques suscités jusque là voient alors leurs nombres augmenter de manière impressio. On retrouve les algogénétiques, ou plutôt les algoriévolutionnaires au sens large, dans un nombre d’applications considérable [Mitchell, 1997]. Les domaines d’applications sont aussi variés que la gestion de gazoducs [Goldberg, 1987], le contrôle actif de vibration [Curtis, 19991], l’optimisation de la combustion dans des fourneaux [Fogarty,1990] , ou la charge des réacteurs nucléaires [ Back,1997] .Les algorithmes génétiques donnent chaque cas des résultats suffisamment intéressants pour que leur usage soit en train de se généraliser à pratiquement tous les domaines liés a l’optimisation.
0.3 - Evolution, théorie des jeux, et optimisation multi-objectifs
L’analogie avec la biologie, ainsi que la richesse apportée par les échanges interdis-
ciplinaires entre génétique et informatique, sont indiscutablement les facteurs clés de la réussite des algorithmes évolutionaires. Mais ce schéma n’est pas isolé, en ce sens que l’interdisciplinarité se révèle souvent payante. En effet, en amont des modélisations issues de la biologie, nous avons également exploré les outils que propose la théorie des jeux [von neummann et morgenstern,1944]. Cet intérêt est né du fait que pour modéliser de manière plus réaliste certains des problèmes que nous avons été amenés à traiter, nous avons dû-nous
Rendre à l’évidence : une optimisation dans le cadréaliste d’un contexte industriel ne peut faire abstraction de la dimension multi-critères des problèmes. Le terme d’ ingénierie concurrente ” a même été forgé assez récemment pour traduire l’importance considérable que prend l’optimisation multi-critères. Or la théorie des jeux propose justement un panel de formalisation permettant de modéliser les problèmes multi-objectifs [Mckinsey, 1952]. Il existe déjà des algorithmes génétiques qui propose des mécanismes permettant de traiter des problèmes d’optimisations multi- objectifs, mais ils font presque excltaécoopératifs de pareto. Pour mieux tirer parti de l’immense richesse que recèlent les fondements de la théorie des jeux, nous avons construit des algorithmes évolutionnaires qui mêlent outils génétiques et fondement s théoriques comme les équilibres compétitifs de Nash ou les équilibres hiérarchiques de stackelberg [Periaux, 1997].
0.4 -
Algorithmes Génétiques Parallèles et dynamique des populationsUne dernière source d’inspiration, qui apporte elle aussi des éléments nouveaux aux algorithme génétiques est la dynamique des populations. Les études menées dans ce domaine permettent en effet de proposer une modélisation des algorithmes évolutionnaires non plus comme une unique population de grande taille, mais plutôt comme un ensemble de sous populations de taille plus petites. Ce qui mène ensuite à l’élaboration d’un paradigme prometteur, celui des algorithmes génétiques parallèles.
![]()
PRINCIPE DE FONCTIONNEMENT
Ce chapitre s’attache à présenter les principes fondamentaux qui régissent les algorithmes génétiques. Sans entrer dans les détails, il s’agit en fait d’expliquer d’une intuitive la manière dont l’analogie entre évolution artificielle et évolution naturelle s’établit.
- ReprésentationLes algorithmes évolutionnaires constituent une famille d’algorithmes qui s’inspirent
Des lois de la génétique et du principe de la sélection naturelle. Le principe fondateur consiste à considérer tout problème d’optimisation ou de contrôle comme un environnement
dans lequel évolue une population de solutions potentielles. Cette particularité des algorithmes évolutionnaires leur permet d’explorer l’espace de recherche de manière beaucoup plus efficace, puisque c’est une recherche à la fois multidimensionnelle et capable
de déjouer les pièges que constituent les minima locaux.
Chacune des solutions de la population est en effet représentée par une structure digital
(par exemple une chaîne binaire ), qui est l’analogue exact d’un chromosome .
l’évolution s’effectue en mimant les opérateurs de croisement et de mutation, puis en appliquant une sélection grâce à une version informatique du principe darwinien du survival of the fittest. Face à un problème d’optimisation, la première étape nécessite donc de formaliser un certain membre de solutions dans un langage approprié et elles seront ensuite
Considérée comme des individus. Si l’on ne choisit de considérer que des chromosomes de taille fixe, il s’agit de faire correspondre à chaque individu une chaîne de langueur :
n ( x
1 x2 x3 … xn ) qui le codera.Par analogie avec les équivalents génétique, on appellera cette chaîne le génotype de l’individu, mais on y référa également par le terme de chromosome. Comme ces individus sont représentés par un unique chromosome, on parlera d’haploïdie. Xalgorithmes évolutionnaires ! haploïdie les chromosomes sont constitués de gènes ou de caractères.
Les différentes positions sur la chaîne chromosomique sont les loci. Chaque gène peut prendre différentes valeurs, les allèles.
Chaque génotype code donc une solution potentielle. On peut par exemple coder dans une chaîne les dimensions d’une étagère. Mais l’étagère au sens physique du terme est désignée
par le terme de phénotype, qui correspond à la réalisation d’un génotype. Les taxons x1 x2 ……xn peuvent prendre leurs valeurs dans l’alphabet A, qui correspond à l’ensemble des allèles. Les algorithmes génétiques classiques utilisent souvent un simple alphabet binaire
( A=0,1). Mais eu égard à la complexité des problèmes traités et aux précisions nécessaires, d’autres approches privilégient des codages plus complexes, comme le codage réel (A=IR)
[Janikow et michalewicz, 1991].
La structure de base d’un algorithme génétique est la suivante :
1.2 - Algorithme 1 (Description d’un algorithme Génétique simple)
Pour un problème de minimisation J, un algorithme génétique simple de la manière suivante :
(1)
Génération aléatoire d’une population de N individus ;(2)
Evaluation de la qualité du phénotype de chaque individu ;(3)
Sélection d’un couple de parents au moyen d’une procédure appropriée ;(4)
Croisement des deux individus avec une probabilité Pc pour générer deux enfants ;(5)
Mutation des deux enfants avec une probabilité Pm ;(6)
Répéter les étapes 3, 4, et 5 jusqu’à ce que la nouvelle population contienne N individusDans ce modèle, un processus de sélection retient les individus les mieux adaptés et les
transmet à un processus d’exploration qui les utilisera pour créer de nouveaux individus
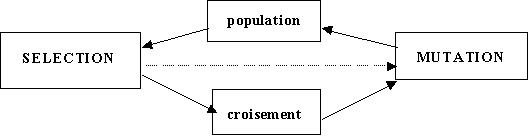
(Donc de nouvelles solutions potentielles au problème qui nous intéresse). La figure 1.1
Représente le schéma de fonctionnement d’un algorithme génétique simple.
Après le processus de sélection intervient un processus de création qui s’inspire également de la génétique puisqu’il fait intervenir les notions de reproduction, de croisement et de mutation. La reproduction consiste à reproduire un individu tel quel dans la génération suivante. Le croisement correspond à la création de deux enfants en combinant les gènes de deux parents choisis par le processus de sélection. Enfin la mutation revient à introduire une modification aléatoire dans le génotype d’un individu.
1.3 - Qualité d’une solution : la fonction de mérite
Le processus de sélection consiste à choisir dans la population P, constituée par l’ensemble des individus, ceux qui semblent les mieux adaptés. Cette notion d’adaptation est inspirée du principe de la sélection naturelle (le célèbre survival of the fittest, qui a lui-même survécu à son auteur). Pour construire un algorithme évolutionnaire, il est donc nécessaire d’imiter aussi bien que faire se peut ce concept de survie des plus adaptés, qui est la clé de voûte de l’approche Darwinienne. La solutionretenue par la plupardes chedans le domaine consiste à associer à chaque individu une fonction de mesurant la qualité dudit individu, la fitness fuction ou la fonction de mérite. Cette fonction de mérite correspond à l’adéquation de la solution au problème considéré. De cette manière, il devient possible de comparer les différents individus, avec toujours à
 l’esprit l’idée de favoriser l’émergence des meilleurs.
l’esprit l’idée de favoriser l’émergence des meilleurs.
FIG. 1.1 – principe de fonctionnement d’un AG
1.4 - fonction de mérite implicite
Un des principaux problème des algorithmes génétiques est justement de construire une fonction de mérite qui soit pertinente. L’élaboration d’une telle fonction dépend bien évidement du problème envisagé, et elle nécessite souvent l’existence de connaissances sur le domaine ou la mise au point d’heuristique complexe. On notera cependant que certaines écoles arrivent à s’affranchir de la notion de fonction de stricto sensu, ou du
Moins parviennent d’avoir à la définir de manière explicite [Dessalles, 1996].
On peut à titre d’exemple les travaux effectués en vie artificielle [Langton,1989]
L’idée d’un environnement comme tierra par exemple consiste à créer des organismes digitaux pour lesquels le temps CPU des ordinateurs sur lesquels il est installé est de l’énergie alors que la mémoire représente les ressources [Ray, 1991,1996].
Ces organismes synthétiques se livrent en fait une véritable bataille pour survivre [Dewdney, 1984]. On pourra également se rapporter à [Dawkins, 1976] pour ses travaux relatifs aux
Biographes. Un autre paradigme puisant directement son inspiration dans la biologie est celui des réseaux neurones artificiels [Bergman, 1989], qui se décline également sous la forme des réseaux neurones évolutionnaires [Yao et , 1998].
Une autre théorie, celle des systèmes immunitaires artificiels, n’est pas sans rappeler les algorithmes évolutionnaires puisqu’elle est également inspirée du monde du v[Perelson, 1989, Forrest et perelson, 1991]. Et comme pour les programmes de vie artificielles, la définition d’une fonction de mérite n’est nécessaire [Wilson, 1985].
On pourra également se reporter à [varela, 1994] pour une étude de l’approche prospective.
- Taille de la populationLe choix de la taille de la population est un des paramètres les plus importants d’un algorithme évolutinnaires [goldberg, 1986]. Et par-là même, c’est l’un des problèmes majeurs
De nombreuses études ont été menées pour essayer de cerner la taille optimale de la population, mais sans obtenir de résultats vraiment généralisables [Alender, 1992, reeves,1993].Certaines approches proposent des tailles de population variables, qui évoluent au cours du temps [Arabas, 1994]. La principale originalité de ce modèle est d’être plus proche de la réalité. En lieu et place d’une population de taille fixe où la fonction de mérite sert à la sélection, il propose plutôt d’indexer l’espérance de vie d’un individu à sa fonction de mérite. Les meilleurs individus reçoivent bien sûr une espérance de vie supérieure à celle des moins bonnes solution. Au fur et à mesure que la population évolue, les individus vieillissent
Et finissent par mourir lorsqu’ils arrivent au terme de leur espérance de vie. Dans ce modèle,
La taille de la population varie donc de manière dynamique en fonction de l’espérance de vie des individus que la composent.
On trouvera dans le chapitre II.1 une étude détaillée de la mise en place de population de très petites tailles. Cette manipulation a principalement pour but d’accéder la convergence de l’algorithme. Un des avantages supplémentaires est qu’elle permet également d’implémenter une version efficace d’un algorithme génétique parallèle.
![]()
Codage binaire
C
e chapitre est consacré aux algorithmes génétiques à codage binaire, et donne quelque uns des fondements théoriques sur lesquels ils s’appuient. Le codage binaire est non seulement la manière la plus simple, mais aussi la plus répondue, de représenter un chromosome dans un contexte informatique. De plus, une analogie assez naturelle s’établit entre les 0 et les 1 de laReprésentation binaire et les bases qui codent l’ADN par exemple.
On trouve également une vue d’ensemble des différents opérateurs de sélection.
Croisement et mutation, avec quelque unes des variations qui se sont développées au cours du temps. Enfin, une section est consacrer à une présentation sommaire des Evollutionary Strategies et de l’Evolutionary Programming.
-ReprésentationLa première étape de la mise en œuvre d’un algorithme génétique consiste à construire une représentation des solutions potentielles aux problèmes. La représentation la plus fréquente est la représentation binaire, en particulier parce qu’elle se prête bien aux recherches théorique. Supposons que l’on ait à résoudre un problème d’optimisation où le paramètre est x
Et où la fonction de mérite (également appelée fonction de coût en optimisation classique) est
j =f(x).
On commence par coder le paramètre x sous forme d’une chaîne binaire de longueur n dépend
Du domaine de variation de x et du nombre décimal dont on a besoin.
Définition 1
Soit d le nombre de décimales désirées (la précision).
Soit xmax et xmin les bornes supérieure et inférieure de l’intervalle de variation pour x
Soit n la taille minimale de la chaîne binaire.
n est alors le plus petit entier tel que :
![]()
ainsi, pour x Є [-1.28,1.28], si l’on veut une précision de 2 décimales, il faudra prendre n=8
pour le codage. En effet, comme :
![]()
On en déduit que n=8 est le plus entier qui satisfasse la relation.
Quand n =8 et x Є [-1.28,1.28], la chaîne binaire 00000000 correspondra alors à la borne inférieure xmin = -1.28 alors que 11111111 représentera la borne supérieure xmax = 1.28.
Les valeurs intermédiaires sont linéairement réparties entre les deux borne. de ce fait, on peut associer une valeur de x à n’importe quelle chaîne de longueur n = 8, grâce à la formule suivante :
![]()
La représentation binaire présentée ici est la plus simple, et a donné lieu à de multiples variantes. A titre d’exemple, [Goldberg, 1991] est le premier parlé de messy genetic
Algorithms, pour lesquels le codage se fait par une séquence binaire de taille variable et non plus fixée arbitrairement. Plusieurs travaux ont également été amenés dans le but d’exploiter plus avant les complexités de la véritable structure chromosomique.
En marge des représentations haploïdes, on trouve quelques travaux qui prônent une structure diploïde. On se reportera à [Greene, 1994, 1996] pour les problèmes d’optimisation stationnaires, et [Goldberg et smith, 1987, wong, 1995] pour la version non-stationnaire. La diploïdie consiste à tenir compte du fait que pour la plupart des espèces, les chromosomes vont par pairies. Les allèles sont donc appariés deux à deux, et un mécanisme intervient. Si le gène dominant est couplé à un gène récessif, seul le gène dominant sera exprimé dans le phénotype final. Pour qu’un gène récessif puisse être exprimé, il doit nécessairement être couplé un gène également récessif. [Levenick, 1991] tente également de se rapprocher encore plus du modèle biologique en insérant des introns dans son codage.
Les gènes expression messy genetic algorithms (GEMGA) proposés par [Kargupta, 1995,1997]
Vont encore plus loin dans l’analogie avec les mécanismes du vivant. Ils s’appuient en effet sur l’expression génétique qui est nom donné au processus de transcription des séquences d’ADN vers les protéines.
La sélection est un opérateur clé sur lequel repose en partie la qualité d’un algorithme évolutionnaire. L’une des principales caractéristiques de tout opérateur de sélection est la pression sélective exercée sur la population. C’est un paramètre d’un maniement délicat, car opter pour une pression sélective trop forte revient à écraser dans l’œuf toute forme de diversité, pour ne garder que le groupuscule d’individu qui le haut du paé. Mais si l’on verse dans l’autre extrême, à savoir une pression sélective trop faible, l’algorithme tend à rapprocher d’une simple recherche aléatoire.
On pourra trouver dans [Dejong, 1975] un travail de pionnier sur l’élaboration et l’évaluation des différents protocoles de sélection. Nous allons présenter dans la suite de cette section quelques-unes des méthodes les plus courantes. Une étude plus approfondie des aspects théoriques, ainsi que certaines variantes plus complexes pourront être trouvées dans
[Baker, 1985,1987].
C’est l’ancêtre de toutes les méthodes de sélection, et elle tire son nom de sa ressemblance avec la roulette ou la loterie. Elle consiste à affecter à chaque individu une probabilité d’être sélectionné proportionnelle à sa fonction de mérite. Pour un problème de maximisation, on
Considère une population de taille N.
Soit : pour i = 1,2,3……. N fi la fonction d’adaptation de l’individu i.
On pose : ![]() La Somme des valeurs des fonctions d’adaptation de l’ensemble des individus de la population. La probabilité Pi qu’à alors
La Somme des valeurs des fonctions d’adaptation de l’ensemble des individus de la population. La probabilité Pi qu’à alors
L’individu I d’être sélectionné est : Pi = fi/F
Il est bien entendu que le modèle le plus simple se fait avec remise, et qu’un individu peut être sélectionné un nombre élevé de fois. De cette manière, les meilleurs individus sont susceptibles de jouer un rôle déterminant dans les générations suivantes. Une certaine diversité est cependant maintenue, car même les individus les moins performants conservent une chance d’être choisis. En effet, ∀i 1≤ i ≤ N, on a Pi>0, ce qui revient à dire que même l’individu le moins adapté au problème considéré (ou en d’autres termes à l’environnement) a une probabilité non nulle d’être choisis. Selon la terminologie proposée par [ba,1], on dira de cette méthode qu’elle est preservative. Cela peut apparaître comme une propriété annexe, mais dés lors qu’on considère des environnements qui évoluent avec le temps, il est crucial de garder en réserve des individus apparemment “inadaptés” car leurs atypisme en fera de précieuses sourde matériel génétique en cas de modification brusque du problème. C’est la une des forces des algorithmes évolutionnaires
La biodiversité, ou du moins son analogue digital. Et même si les conditions du problème ne changent pas, une population uniformément homogène concentrée au niveau d’un optimum local ne peut en sortir que grâce à ces individus atypiques.
La sélection stochastique avec reste s’inspire très fortement de la sélection par roulette, sauf qu’elle y ajoute un léger aspect déterministe. On commence par déterminer la probabilité Pi = fi/F qu’a chaque individu d’être sélectionné. Soit N la taille de la population. On pose alors Mi = N. Pi, où Mi correspond au nombre moyen de copies qu’un individu peut espérer recevoir par une sélection de type roulette. On définit ensuite :
n
i =E(Mi) où E désigne la partie entièrer
i = Mi-E(Mi) les ri sont les restesle caractère déterministe de la sélection stochastique avec reste intervient alors, car on affecte automatiquement à chaque individu ni copies dans la génération suivante.
Comme : ![]()
Il reste en générale un nombre ![]() de copies à affecter pour compléter la
de copies à affecter pour compléter la
Population de la génération suivante. Pour attribuer ces copies restantes, le processus
Utilisé est une roulette classique, qui s’appuie non pas sur les valeurs Pi mais sur les
Restes ri considérons une population de taille N=4 constituée de 4 solutions S1,
S2, S3 et S4, pour un problème de maximisation.
f=10 P1=10/25=0.4 M1=4.0.4=1.6 n1=E(M1)
f=7 P2=7/25=0.28 M2=4.0.28=1.12 n2=E(M2)
f=5 P3=5/25=0.2 M3=4.0.1=0.8 n3=E(M3)
f=3 P4=3/25=0.12 M4=4.0.12=0.48 n4=E(M4)
![]()
On affecte donc une copie à S1 et une copie à S2, mais il reste deux copies à déterminer pour compléter la population.
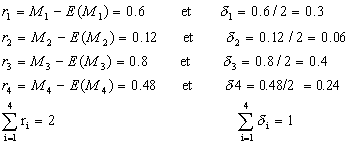
On relance alors une sélection par roulette proportionnelle aux δi. On notera que la solution S3 est désormais la plus avantagée.
Il existe plusieurs versions de cette sélection, qui se différencient principalement par le fait qu’elles se font avec ou sans remise.
Toute une famille de méthodes utilisent une sélection qui n’est pas directement proportionnelle à la valeur de la fonction de mérite, mais dépend plutôt du rang de l’individu
Dans la population. Le classement par rang, ou ranking, a principalement pour but d’éviter que les individus avec des solutions de mérite très élevées ne perturbent le processus stochastique en obtenant un nombre de copies trop important [Whitly, 1989].
Une sélection par tournoi consiste, chaque fois que l’on veut choisir un individu, à sélectionner un sous-ensemble de la population et à ne conserver que le meilleur élément du sous-ensemble. Si T est la taille tu tournoi, on sélectionne aléatoirement T individus dans la population et on les fait entrer en compétition : seul le vainqueur (donc celui qui a la meilleure fonction de mérite) est retenu. Le processus est réitéré N fois, où N est la taille de la population. Cette méthode est caractérisée par une pression sélective en général plus forté que les méthodes proportionnelles (pour qu’un individu peu performant puisse être sélectionné, il faut que ses adversaires soient encore moins bons que lui). Elle donne des résultats particulièrement bons dans les cas où le caractère un peu trop aléatoire de la roulette introduit un biais.
On peut trouver dans [Goldberg, 1990] une variante de Boltzmann d’une sélection par tournoi. Elle rappelle certains aspects du recuit simulé puisqu’elle fait intervenir la température dans la détermination du vainqueur du tournoi.
Le modèle élitiste consiste à recopier automatiquement le meilleur individu de chaque génération dans la suivante. En effet, le caractère aléatoire de la sélection fait que rien ne garantit que la meilleure solution soit conservée. L’élitisme permet donc de s’assurer que la meilleure solution de chaque génération ne peut que s’améliorer avec le temps. Le modèle élitiste n’est pas une méthode de sélection en soi, mais plutôt une variante qu’on ajoute aux méthodes déjà citées.
2.2.6-sélection par troncature
il existe également des algorithmes évolutionnaires qui considèrent que la sélection ne doit
pas être laissée au hasard. Ainsi, les breeding genetic algorithms, développés par [schlierkam-pvoosen, 1993] s’inspirent des méthodes de sélection utilisées par les éleveurs. L’une des plus classique étant la sélection par troncature (truncation selection) où on choisit de manière déterministe les T% meilleurs individus d’une génération pour générer la suivante. Cela revient en quelque sorte à généraliser le modèle élitiste à tout le processus de sélection.
Le croisement est le premier opérateur qui intervient au niveau de processus de création. Il vital, en ce sens que c’est grâce que s’effectuent les échanges d’information au sein de la population. Chaque fois qu’un individu est retenu par le processus de sélection, on détermine aléatoirement s’il doit participer à un croisement (avec une probabilité Pc) ou être transmis directement à l’opérateur de mutation. Dans le second cas, on parle de reproduction, car l’individu est reproduit tel quel dans la génération suivante.
Soit J un individu choisi par l’opérateur de sélection. Soit Rj un nombre aléatoire,
0 ≤ Rj ≤ 1. On a:
Si Rj ≤Pc alors appliquer l’opérateur de croisement sur j
Si Rj>Pc alors appliquer l’opérateur de reproduction sur j
Le croisement est la manière la plus répandue de créer de nouveaux individus : on choisit deux individus (les parents) et on les combine pour en générer deux autres (les enfants).
Cette combinaison utilise la notion de points de coupures qui correspond aux loici au niveau desquels s’effectuera l’échange de matériel génétique.
croisement simple à un pointpoint de coupure
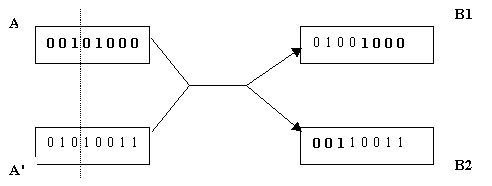
FIG. 2.1 opérateur de croisement, un seul point de coupure
Le croisement à un point est l’opérateur de croisement le psimple et le plus. Il consiste à sélectionner un point de coupure, puis à subdiviser le génotype de chacun des parents en deux parties de part et d’autre part de ce point. Les fragments obtenus sont alors échangés pour créer les génotypes des enfants. Ainsi, la figure 2.1 ésente le cas où le point de coupure tombe après le troisième locus ; les parents A et A’ produisent alors les enfants B1 et B2.
points de coupure
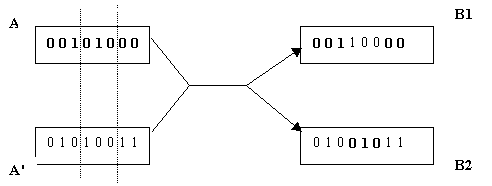
FIG : 2.2- opérateur de croisement à deux points de coupures
Le croisement multi-points est une généralisation du croisement à un point en ce sens qu’au lieu de choisir un seul point de coupure, on en sélectionne k. l’intérêt d’une telle approche apparaît rapidement, car il devient possible en un seul croisement d’échanger des building
blocks qui sont situés au milieu du chromosome sans avoir à procéder par étapes. Bien sur la contrepartie est que c’est une technique qui est plus destructrice par rapport à ces même building blocks, puisqu’ils peuvent se retrouver scindés en plusieurs fragments sans intérêt. La figure 2.2 représente un croisement à deux points, dans le cas où les points de coupure tomberaient après les troisièmes et cinquième loci : les parents A et A’ produisent alors les enfants B1 et B2.
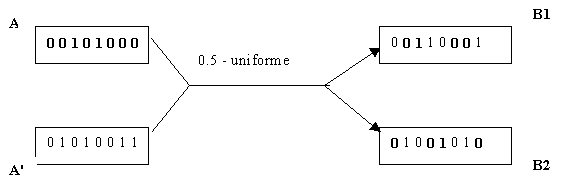
FIG.2.3- exemple de croisement 0.5-uniforme
Les fondements théoriques du croisement uniforme ont été posés par[Syswerda, 1989].
Soient A et A’ les parents, et B1 et B2 les enfants. Pour chaque locus de B1, on détermine aléatoirement (avec une probabilité P) si ’allèle est fourni par A ou par A’. Le second enfant B2 se voit affecter l’allèle du parent qui n’a pas été retenu. Si B(k) dénote la valeur de l’allèle au niveau du locus k pour le chromosome B, n la langueur du chromosome et r un nombre aléatoire, avec
![]() , on a :
, on a :
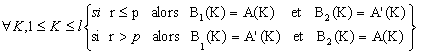
La fi2.3 montre un exemple de croisement 0.5-uniforme (chaque parent a une chance égale de transmettre son allèle à chacun des enfants pour tout les locis ). [Spears et Jong, 1991] proposent une analyse détaillée des croisements p-uniformes.
Pour ce qui est des valeurs optimales du taux de croisement Pc, on pourra se référer à [Eshelmant, 1989].
Il est généralement admis que les valeurs de Pc comprises entre 0.8 et 0.95 donnent les résultats les plus satisfaisants dans la plus plupart des cas.
Certains problèmes nécessitent cependant la mise en ouvre de représentations particulières
Plus complexes, de type matriciel par exemple. Dans ce cas, les opérateurs de croisement sont également plus complexes mais obéissent néanmoins à un principe commun, l’échange d’information entre individus.
Il est à noter que si les croisements présentés ici mettent tous en jeux deux parents, ce n’est pas toujours le cas. Il existe en effet des opérateurs de croisement qui font intervenir trois parents, voire plus, les croisements multi-parents [ Eiben, 1994]. [Ackley,1987] a par exemple introduit un croisement par vote, que [Muhlenbein, 1989] a ensuite développé en
p-sexual voting recombination, ou recombinaison sexuée par vote à p parents.
La mutation est une modification aléatoire de la valeur d’un gène qui se produit avec une probabilité fixée. Elle primordiale puisqu’elle donne la garantie que tout point de l’espace
de recherche peut être atteint lors du processus d’exploitation. Si Pm est la probabilité de mutation, 0≤ r ≤ 1 un nombre tiré au hasard et que l’on ait r < Pm pour le quatrième locus par exemple, alors :
allèle a muter

FIG. 2.4 - opérateur de mutation
Comme pour le taux de croisement, la recherche d’un taux de mutation optimal a suscité de nombreux travaux . On retiendra juste que les valeurs classiques de Pm oscillent entre 0.001 et 0.01.
2.5-Résultats théoriques : le théorème des schémas
Une des raisons qui font des algorithmes génétiques binaires une modélisation fort appréciée est qu’ils se prêtent bien à certaines manipulations formelles. Un des exemples les plus communément cités dans la littérature sur les algorithmes génétiques est par exemple le théorème de schémas. Il s’appuie sur la notion de schémas utilisée par HOLLAND,1975.
Définition 2 (schémas
)Un schémas est une séquence binaire enrichi de symbole, qui correspond à une valeur indifférente, 0 ou 1. Ainsi pour le schémas (0*00*0) représente les 4 séquences binaires suivantes :
(000000)
(010000)
(000010)
(010010)
Définition 3 (ordre d’un schémas)
L’ordre d’un schémas est le nombre de positions instanciées. Si n est la langueur d’un schémas S et m le nombre de positions occupées par des *, alors l’ordre 0(s) du schémas
Est :
O(s) = n - m
Définition 4 (longueur utile d’un schémas)
La longueur utile λ d’un schéma est la distance entre la première et la dernière position instanciées. Un schémas S = (*10**00**) a pour longueur utile λ(s) = 7 – 2 = 5.
Définition 5 (fonction de mérite d’un schémas)
La fonction de mérite d’un schémas est la moyenne des fonction de mérite des chaînes binaires qu’il représente.
Théorème 1 (théorème de schémas)
Les schémas dont la longueur utile et l’ordre sont faibles, et dont la fonction de mérite est meilleure que la fonction de mérite moyenne de population reçoivent un nombre de copie qui
Croit de manière exponentielle au cours des générations d’un algorithme génétique.
Il est également possible d’exprimer ce théorème de manière plus formelle pour un algorithme génétique simple. Soit P(k) la population à la génération k, N le nombre d’individus de la population, et c(S,K) le nombre de copies du schémas S dans la population P(k).
En admettant une sélection par roulette, l’application de l’opérateur de sélection donne :
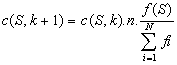
Où F(S) est la fonction de mérite du schéma S, alors que F’ est la fonction de mérite moyenne de la population P(k).
Soit un opérateur de croisement simple à un seul point de coupure, et Pc la probabilité de croisement uniforme répartie. Cet opérateur détruit un schéma de longueur utile λ(S) avec
Une probabilité Pd égale à :
![]() Le schéma S survit donc à l’opération de croisement avec une probabilité:
Le schéma S survit donc à l’opération de croisement avec une probabilité:
Ps = 1 – PcPd.
Après les phases de sélection, on donc :
![]()
Soit Pm la probabilité de mutation d’un gène instancié (donc différent de *) de S, et o(S) l’ordre de S. le schéma S ne sera pas affecté par l’opérateur de mutation avec une probabilité :
![]() Or Pm étant très proche de 0, on a :
Or Pm étant très proche de 0, on a :
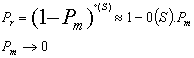 Ce qui signifie que S est modifié par la mutation avec une probabilité 0(S).Pm.
Ce qui signifie que S est modifié par la mutation avec une probabilité 0(S).Pm.
L’application successive des opérateurs de sélection, croisement et mutation donne en fin de compte la formulation qui à l’origine du théorème des schémas:
![]() Ce qui revient à dire que les schémas ayant une fonction de mérite supérieure à la moyenne,
Ce qui revient à dire que les schémas ayant une fonction de mérite supérieure à la moyenne,
Une longueur utile et un ordre faible, reçoivent un nombre de copies qui croit de manière exponentielle.
Définition 6 (building blocks)
Un algorithme génétique construit des solutions optimales ou quasi-optimales en juxtaposant
Des schémas courts, d’ordre faible, performants, qu’on appelle les building blocks.
Les résultats théoriques concernant les propriétés des algorithmes génétiques sont tous fondés sur une tentative de modélisation formelle. La plus classique est sans doute une modélisation par chaîne de MARCOV, qui fournit un cadre mathématique adapté aux algorithmes génétiques.
[Cerf,1994] en particulier propose une formalisation poussée des algorithmes génétique s’appuyant sur un modèle MAKOVIEN. Il fait de plus appel à des outils mathématiques très élaborés comme la théorie de FREIDLIN-WENTZELL. Cette théorie vise à formaliser les petites perturbation aléatoires de système dynamiques.
En combinant ces deux modèle, CERF considère les algorithmes génétiques comme une perturbation aléatoire d’un mécanisme de sélection trèrudimenta[Cerf, 19]. Il analyse
La manière dont l’intersection asymptotique entre les mutations et la force de sélection entraîne la convergence de l’algorithme vers les maxima globaux de la fonction d’adaptation.
Il montre en particulier que lorsque la taille de la population est plus grande qu’une certaine valeur critique, fortement dépendante du problème, l’interaction assure la convergence de l’algorithme (en un temps éventuellement fini) ces résultats comptent parmi les premiers résultats mathématiques se rapportant à la convergence des algorithmes génétiques.
CHAPITRE 3
Codage réel
C
e chapitre est dédié aux algorithmes évolutionnaires à codage réel, et s’attache à souligner leur spécificité, leurs avantages et leurs inconvénients. En effet, le codage binaire est bien adapté à certaines domaines, principalement parce qu’il facilite la mise au point résultats théoriques. Mais la puissances algorithmes génétiques ne dépend pas du codage binaire [Goldberg, 1990a].[Deb et Goldberg, 1989b] montrent en particulier que l’une des caractéristiques qui fait la force des algorithmes génétiques, à savoir le parallélisme implicite (voir [Dessalles, 1996]), n’est absolument pas dépendant de la représentation binaire. Il existe de nombreux problèmes où un codage réel est plus approprié et donne de meilleurs résultats [Michalewicz, 1991].On trouvera également une présentation sommaire de deux approches qui ont choisi le codage réel dés le début, les stratégies d’Evolution et Programmation Evolutionnaire.
La représentation des solutions dans le cadre d’un algorithme génétique n’est pas nécessaire réduite à un alphabet de faible cardinalité, comme l’alphabet (A=0.1)
Présenté dans le chapitre précédent. Il existe en effet toute une école pour laquelle la représentation la plus efficace est celle qui s’appuie sur des nombres réels, avec (A=IR)
Cette différence de position a parfois pris des aires de querelle de clocher, opposant les puristes la théorie, surs la faible cardinalité était la solution, et les partisans du codage réel, qui pouvait montrer preuves à l’appui que les résultats étaient meilleurs pour de nombreuses applications réelles. [Gldberg, 1990] propose une explication à ce paradoxe apparent en s’appuyant sur la notion d’alphabet virtuel : il postule que quelle que soit la taille
De la l’alphabet de départ, l’espace de recherche est rapidement ramené à un sous-espace qui
Peut, lui, être représenté par un alphabet de faible cardinalité. On pourra noter que le parti pris d’un codage réel a été adopté dès le début par l’école allemande des Evolution Strategies
[Rechenberg, 1973]. [Michalewicz, 1992] propose une étude détaillée des algorithmes génétiques avec codage réel, soulignant en particulier leur robustesse dans le cas d’applications considérées comme difficiles pour des algorithmes génétiques binaires.
l’opérateur de croisement pour le codage réel est très proche de celui décrit pour le codage binaire dans la section 2.3. soient A et A’ les parents qui ont été choisis par le processus de
sélection. Ils génèrent deux enfants B1 et B2. Si on considère par exemple que c’est un croisement avec deux points de coupures, et que ces points de coupure tombent respectivement après le troisième et le cinquième loci on a :
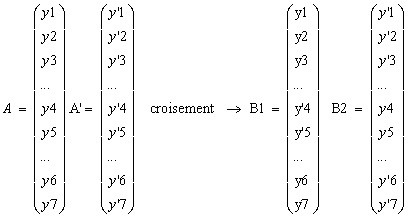
Bien évidement, les Y'I son ici tous des réels, non plus des chaînes binaires codant des réels.
Le croisement parait d'être le même que dans le cas du codage binaire, mai il existe de fait une différence fondamentale : dans le cas réel, le point de coupure tombe nécessairement
Entre deux variables alors que la manière dont sont codées les variables en binaire fait que le point de coupure peut tomber à l'intérieure d'une variable. Pour le codage réel, le croisement s'apparente donc plus à une simple permutation des valeurs de variables existant déjà.
Il n'y a donc jamais de création de valeurs nouvelles. De ce fait, l'espace de recherche est limité aux
![]() combinaisons possibles des allèles des parents.
combinaisons possibles des allèles des parents.
Le codage réel permet cependant de développer naturellement toute une série de nouveaux types de croisement, principalement à base de combinaison linéaire des deux vecteurs considérés. On peut trouver dans [Davis, 1993] une étude du croisement arithmétique. Si A et A' sont les parents retenus par le processus de sélection et B1 et B2 les deux enfants qu'ils génèrent, alors le croisement arithmétique est défini par :
B1= α . A+ (1-α). A'
B2= α .A'+ (1-α).A avec ![]()
Pour un algorithme génétique binaire, l'exploration se fait principalement grâce aux croisements, par le biais des échanges de building blocks. De ce fait, la mutation est souvent considérée comme un processus secondaire dans la plus part des cas. On a vu que l'opérateur de croisement pouvait créer de nouvelles pour les variables. C'est cette raison qui donne à la mutation une importance prépondérante en codage réel, car c'est elle qui assurera une partie importante du processus d'exploration.
Si les croisements sont assez similaires dans le des algorithmes génétiques binaires et des algorithmes génétiques réels. La mutation est en revanche complètement différente. Il ne suffit plus d'inverser un bit. Un certain nombre d'opérateurs de mutation existent, et nous avons utilisé la mutation non- uniforme.
Si un gène yi doit subir une mutation, alors la nouvelle valeur yi' de la variable sera aléatoirement générée dans l'intervalle [Mmin, Mmax], où Mmax et Mmin sont les bornes supérieures et inférieures de la variable yi :
Yi'= yi+Δ(t, Maxi-yi) si θ=0
Y'i= yi-Δ(t, yi-Mini) si θ=1
t, correspond au nombre de générations écoulées
θ, est un booléen aléatoire
La fonction Δ(t, y) quant à elle peut être défini par :
Δ(t, y)= y.r.![]()
y, est la variable a muter
r, est un nombre aléatoire dans [0, 1]
t, correspond au nombre de générations écoulées
T, est le nombre maximal de générations autorisées
b, est un paramètre de raffinement (ou de non-uniforme).
La fonction Δ(t, y) est construite de manière à renvoyer une valeur dans l'intervalle [0,y]. de plus la probabilité que Δ(t, y)tende vers 0 doit augmenter lorsque t augmente. Cette dernière contrainte permet à l'opérateur de mutation, après qu'un certain nombre de génération se soit écoulé, d'affiner les solutions trouvées lors de la phase d'exploitation.
On peut également préférer une version plus complexe de Δ(t, y), comme par exemple :
Δ(t,y) = y.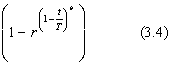
En utilisant la version la plus simple de Δ (eq. 3.3), l'équation 3.2 devient :
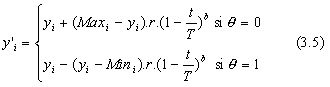
Durant les premières générations, on a ![]() l'équation 3.5 donne alors :
l'équation 3.5 donne alors :
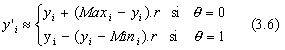
pour θ=0 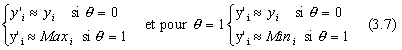
puisque r est aléatoirement généré dans [o, 1], il est claire que
![]() peut prendre toutes les valeurs comprises dans
peut prendre toutes les valeurs comprises dans ![]() . La mutation ainsi définie permet donc à l'algorithme d'aller en n'importe quel point de l'espace de recherche : c'est la phase d'exploration. En fait d'optimisation, on a
. La mutation ainsi définie permet donc à l'algorithme d'aller en n'importe quel point de l'espace de recherche : c'est la phase d'exploration. En fait d'optimisation, on a
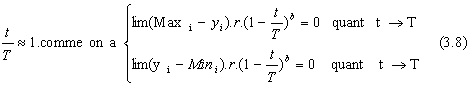
on pose
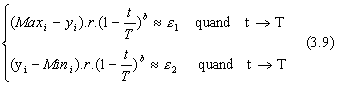
L'équation 3.5 se réécrit alors :
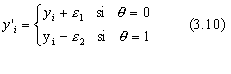
Quand t tend vers T, l'ampleur des mutations devient très faible, puisque les nouvelles valeurs sont égales aux anciennes à un
![]() prés. Ce comportement est entièrement voulu, car il permet à l'algorithme d'affiner les résultats obtenus lors de l'exploration : c'est la phase d'exploitation.
prés. Ce comportement est entièrement voulu, car il permet à l'algorithme d'affiner les résultats obtenus lors de l'exploration : c'est la phase d'exploitation.
La mutation non-uniforme constitue donc un compromis intéressant entre deux buts clairement concurrents, l'exploration de l'espace de recherche et l'exploitation des solutions obtenues.
Introdu
Hollanest souvent considéré comme le père fondateur des algorithmes évolutionnaires [holland,1975]. Mais il faut néanmoins spécifier qu'à peu prés à la même époque est née en Allemagne une technique s'inspirant également des théories de l'évolution, les evolutionsstrategies(ES)[Rechenberg,1973,Schwefel,1981].Ce qui fait l'intérêt des ES, c'est qu'elles ont été conçues avec à l'idée des utiliser comme optimiseurs, alors que Holland ne s'intéressait par particulièrement à l'optimisation, mais plutôt à l'adaptation.
Stratégie d'évolution (μ, k, λ, ρ)
Nous allons présenter dans cette section la version la plus générale d'ES [Back, 1997].
Dans les premiers temps des ES, trois différentes formes coexistaient :
le symbole μ représente le nombre de parents à un moment donné dans la population. Le symbole λ reprιsente quant à lui le nombre d'enfants que génère les μ parents au cours d'une génération. La déférence entre ces versions concernent la manière dont les parents de la génération suivantes sont sélectionnés.
En effet, pour la stratégie (μ+λ), les μ parents sont mélangés aux λ enfants, et on ne retiendra
Pour la génération suivante que les μ individus les plus adaptés de cet ensemble de cardinal (μ+λ), μ comme λ peuvent prendre des valeurs aussi petites que 1.
C'est le cas par exemple pour la stratégie (μ+λ), mais c'était encore plus vrai au tout début des
ES, qui utilisaient une stratégie (1+1).
En revanche, pour la stratégie (μ,λ), où λ>μ≥1, les μ individus de la nouvelle population sont
Nécessairement sélectionnées parmi les λ enfants, même s'ils sont moins bons que les parents.
Cette stratégie implique que chaque individu ne peut avoir un enfant qu'une seule fois avant d'être écarté.
C'est donc une différence fondamentale avec la version (μ+λ) où un individu peut vivre éternellement si aucun enfant ne se montre meilleur. Pour éviter que ce genre ne se produise, la version la plus complète (μ, k, λ) introduit un paramètre k≥1 qui correspond à la durée de vie d'un individu ( donc le nombre d'itérations durant lesquelles il est conservé dans la population ).
La version (μ,λ) peut donc être vue comme une instanciation de (μ, k, λ) avec k=1, alors que (μ+λ)correspond à k = ∞.
La version la plus récente des ES un certain nombre de nouveaux paramètres, et en particulier:
la stratégie d'évolution (μ, k, λ, ρ) peut alors être définie par le 19-uplet suivants:
![]()
![]()
avec:


un ES simple peut être décrit par l'algorithme suivant:
Algorithme 2 (ES (μ,λ) et ES(μ+λ) )

3.4.2-Evolutionary Programming
Une autre approche appelée Evolutionary programming a été également développée par
[Fogel, 1966].
A l'origine, les individus de la population étaient représentés comme des automates à états finis
Le but de cette technique était de développer un individu capable de prédire un changement dans son environnement. Plus tard, elle a été étendue pour pouvoir traiter des problèmes continus
Cette approche a certains points communs avec les ES comme avec les algorithmes génétiques.
Les principales caractéristiques des EP est qu'il n'existe pas d'opérateur de croisement. Comme pour les ES, c'est la mutation qui joue un rôle primordial. Les EP utilisent en revanche une méthode de sélection probabiliste du type tournoi, alors que les ES utilisent plutôt une sélection par troncature. Un algorithme EP type peut se formuler de la manière suivante:
Algorithme 3 (Evolutinary programming)

![]()
CHAPITRE 4
*************** Optimisation d'un multiplicateur ******************
RESUME
On considère l’optimisation d’un multiplicateur par la programmation mathématique et les Algorithmes Génétiques (AGs). Un problème statique est d’abord résolu en utilisant SLP (Sequential Linear Programming), puis la maximisation de la première fréquence propre est obtenue par le placement de raidisseurs avec les AGs. L’efficacité de ces derniers est testée en comparant les résultats finaux d’optimisations séquentielles SLP / AGs à une optimisation globale par les AGs comprenant toutes les contraintes statiques et dynamiques du problème.
ABSTRACT
The optimization of a gearbox is considered here. It is performed using mathematical programming and Genetic Algorithms (GAs). A static problem is first solved using SLP (Sequential Linear Programming), then the first natural frequency is maximized locating stiffeners using GAs. The efficiency of the GAs is tested comparing the final results from some sequential optimizations SLP / GAs to a global optimization based on GAs incorporating the static and dynamic constraints of the problem.
I . INTRODUCTION
Une des difficultés majeures rencontrées dans le domaine de l’optimisation est la spécificité ou les limitations des algorithmes qui ne se révèlent performants que pour des classes de problèmes précises. L’exemple de l’utilisation d’algorithmes basés sur les gradients ( SLP, SQP, Directions Réalisables…) (Haftka, 1992) pour des problèmes dont les fonctions objectifs et contraintes doivent êtres dérivables en est l’exemple le plus criant. Par extension ces méthodes ne sont applicables qu’aux problèmes à variables continues, occultant de ce fait tout le panel de problèmes discrets, courants en mécanique. Parmi les méthodes « dédiées » aux problèmes discrets, on trouve les algorithmes génétiques (Goldberg,1973) dont la capacité à converger et leur indifférence aux irrégularités des fonctions ont grandement contribué à leur succès. Des problèmes de positionnement de raidisseurs (Fatemi
, 1998) ou d’actionneurs (Furuya,1993), dedétermination des séquences d ‘empilement de plis pour les matériaux composites (Le Riche, 1993) ont été traités avec de telles méthodes. Ce travail propose d’évaluer la capacité des Algorithmes Génétiques à se rapprocher de la solution optimale d’un problème mixte à composantes continues et discrètes. En possession d’outils dédiés aux problèmes continus et d’autres aux problèmes discrets, la solution d’un problème mixte serait obtenue par la répétition de séquences d’optimisation du type (problème continu / problème discret) jusqu’à convergence (figure 1)
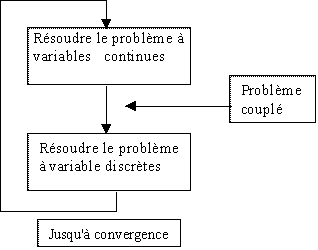
Figure 1 :
Convergence d’un problème (continu / discret)
Cette étude a pour but principal de tirer des conclusions sur le comportement et la pertinence des Algorithmes Génétiques utilisés pour l’optimisation d’un multiplicateur simple servant comme base de travail. Un problème statique en variables continues et un problème dynamique purement discret sont définis. Le mécanisme considéré est tel que le couplage entre les deux problèmes est faible. Ceci permet d’obtenir une solution en trois étapes (continue / discrète / continue) à laquelle nous pouvons confronter les Algorithmes Génétiques pour la résolution du problème mixte dans sa globalité.
II . PRESENTATION DU MODELE ET DU PROBLEME D’OPTIMISATION
II .1 Le modèle
Le multiplicateur considéré possède deux pignons à denture hélicoïdale (figure 2). L’angle d’hélice de la denture est fixé à 11.35° et l’angle de pression à 20°. Un couple d’entrée de 75 Nm est imposé sur la roue menante. De par la présence de la denture hélicoïdale, ce chargement a deux effets majeurs: - Un déplacement axial relatif des deux roues. - L’apparition de contraintes au sein du carter. Afin de modéliser ce comportement, un modèle éléments finis simplifié a été construit grâce au code de calcul ANSYS (Swanson Analysis System Inc) (figure 3). Le modèle, composé d’éléments poutres et coques, est tel que effets de la denture hélicoïdale précédemment cités sont pris en compte. Cela évite ainsi la construction d’un modèle volumique relativement gourmand en temps de calcul pour une procédure d’optimisation.
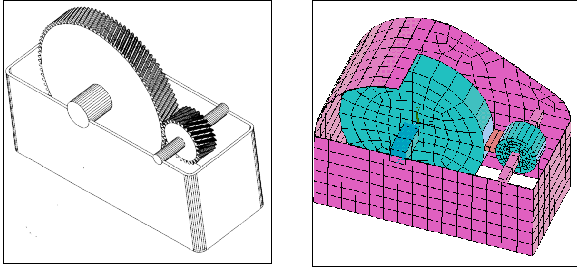
Figure 2 Figure 3
Multiplicateur à denture hélicoïdale Modèle Eléments finis
II . 2 Problème d’optimisation
Nous proposons de minimiser la masse du multiplicateur sous les contraintes
suivantes :
- Le déplacement axial relatif entre les deux pignons (
Δ z) est limité à 1 mm.- La contrainte de Von Mises sur le Carter est limitée à 150 MPa.
- La première fréquence propre du multipldoit être supérieure à 105Hz.
Les variables utilisées et leurs bornes sont :
5 mm
≤Diamètres des deux arbres ≤30 mm5 mm
≤ Une épaisseur pour les deux roues ≤ 40 mm2 mm
≤ Epaisseur du carter ≤ 5 mmOn appellera Problème I, le problème continu ne comportant que les contraintes statiques
et Problème II, le problème dynamique de nature discrète.
III .
SOLUTION PAR APPLICATION SEQUENTIELLE DE LA METHODE SLP ET LA METHODE AGIII . 1 Solution du Problème I par SLP
L’utilisation de la méthode par linéarisation séquentielle fournit les résultats suivants
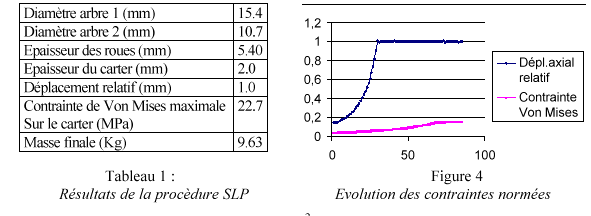
Le design obtenu rend la contrainte de déplacement active alors que la contrainte de Von Mises n’atteint que 19 % de la contrainte maximale autorisée (Figure 4). Sur ce design obtenu on cherche à obtenir des fréquences propres au delà de la plage d’utilisation du multiplicateur comprise entre 0 et 105 Hz. La première fréquence propre du multiplicateur obtenue étant de 43.2 Hz. A cet effet, on vient placer des raidisseurs sur le carter grâce aux Algorithmes Génétiques.
III . 2 Solution du Problème 2 par les Algorithmes Génétiques
Soient cinq raidisseurs à disposer le long du carter, et ce en 16 positions discrètes définies par le maillage élément finis. Leur nombre et leurs positions sont tels que la première fréquence propre est maximisée pour une masse totale minimale, ce qui conditionne le nombre de raidisseurs utilisés. Nous définissons alors une fonction objective f de la façon suivante
![]()
 Les coefficients a et b sont choisis de telle sorte à ce que la masse et la fréquence aient un poids comparable sur la fonction objectif.
Les coefficients a et b sont choisis de telle sorte à ce que la masse et la fréquence aient un poids comparable sur la fonction objectif.
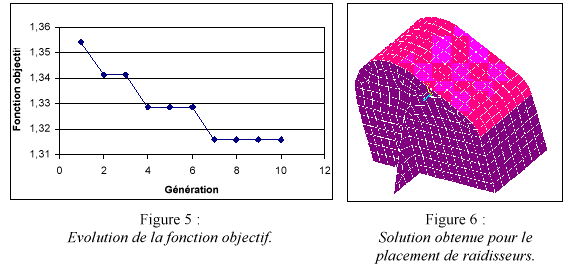
Pour ce problème les valeurs a=10 et b=40 ont été choisies. Une démarche élitiste a été utilisée, c’est-à-dire que le meilleur design d’une génération ( au sens de la fonction objectif définie ci-dessus) est conservée à la génération suivante. Une population de 15 individus avec un taux de mutation de 1% a été employé. La solution obtenue correspond à l’emplacement d’un raidisseur au niveau de l’axe du grand pignon (position A) (figures 5 et 6).Ce résultat peut être interprété par le fait que le grand pignon représente la plus grande masse dans le système. Le premier mode correspond alors à une translation axiale de ce pignon. La maximisation des fréquences propres est donc obtenue en localisant un raidisseur vis à vis de l’axe du grand pignon. Ce raidisseur a pour effet de totalement modifier le problème statique, il faut donc relancer l’optimisation continue.
III . 3 Solution du Problème I avec le(s) raidisseurs placé(s).
L’optimisation par SLP du Problème I avec le carter raidi fournit les résultats suivants
(Tableau 2).

Là encore la contrainte de déplacement devient active et la contrainte de Von Mises
obtenue reste faible.
III . 4 Doit-on continuer le processus ?
L’optimisation continue effectuée sur le multiplicateur dont le carter a été raidi ne nécessite pas de chercher à repositionner des raidisseurs. En effet, les variables utilisées sont telles que le problème «maximiser la 1er fréquence propre avec le nombre minimal de raidisseur » trouve toujours sa solution dans le positionnement d’un raidisseur au niveau de l ‘axe du grand pignon. On est alors certain qu’après trois itérations, le processus ne permettra plus d’amélioration des problèmes I et II. Ayant atteint par la procédure séquentielle (continue / discret) un « optimum », il est alors intéressant de comparer le résultat final, à ce que trouvent les algorithmes génétiques pour le problème englobant la statique et la localisation des raidisseurs.
IV
. SOLUTION DU PROBLEME GLOBAL PAR LES ALGORITHMESGENETIQUES ET COMPARAISON
Le problème considéré comporte désormais les contraintes statiques et le placement des raidisseurs. Nous recherchons le taux de discrétisation à donner aux variables afin d’obtenir, pour des tailles de population raisonnables, une convergence satisfaisante. Discrétisation en dixièmes de millimètre Les variables de dimensions sont d’abord discrétisées en dixième de millimètre ce qui se rapproche d’un problème à variables continues.
La taille de la population est fixée à 30. Les résultats obtenus avec les Algorithmes Génétiques pour le taux de discrétisation et la taille de population choisis montrent qu’ils ne réussissent pas à converger et ce sur une série de dix essais. Aux vues de l’ampleur du domaine de recherche, ce résultat était prédictible. Discrétisation en millimètres.
Le choix des coefficients a et b pour la pondération des objectifs masse et fréquence est crucial pour l’obtention d’un optimum. En effet, les valeurs des masses et des fréquences et surtout leurs variations relatives ont des ordres de grandeur tout à fait différents. Pour cette raison il n’existe que certains couples (a,b) permettant de se rapprocher de l’optimum.
V. CONCLUSION
Un essai d'optimisation d'un problème mixte (continu / discret) sur un multiplicateur a été effectué. Le problème, d'abord résolu séquensiellement par SLP puis les algorithmes génétiques. Ces derniers se sont révélés efficaces pour des taux de discrétisations des variables par pas d'un millimètre, la population comprenant 30 individus. l'étude montre aussi que les choix des coefficients de pondération sont essentiels pour aboutir à l'optimum.
![]()
chapitre 5
Conclusion
Dans ce mini-projet, nous avons essayé de mettre à la portée dugroupe productique, þþles outils nécessaires pour qu'ils puissent comprendre le principe de fonctionnement d'un
algorithme génétique, et de les permettre voir de pris l'une des méthodes efficace face à un problème d'optimisation.
Pour cet intérêt, nous avons également, commencé par une introduction a fin d'expliquer, les trois formes d'intelligence humaine, et de faire les liens entre intelligence naturelle et intelligence artificielle, suivant l'historique de l'évolution de la pensé de l'homme.
Puis dans un premier chapitre nous attaquons le principe de fonctionnement et les fondamentaux qui régissent les algorithmes génétiques, il s'agit en fait d'expliquer d'une manière intuitive la manière dont l'analogie entre évolution artificielle et évolution naturelle s'établit.
Un deuxième chapitre est consacré aux AG à codage binaire, et donne les fondements théoriques sur lesquels ils s'appuient. On trouvera également une vue d'ensemble des différents opérateurs de sélection, croisement, et mutation.
Le troisième chapitre est dédié aux AG à codage réel et leurs avantages surtout dans les applications réelles.
En fin le quatrième chapitre est dédié à un exemple explicatif mais pas détaillé a fin de toucher les dimensions de l'application des algorithmes génétiques dans la mécanique et en particulier dans le domaine de la CFAO.
AN
: n.m Acide désoxyribonucléique, Macromolécule organique qui constitue le support universel de l'information héréditaire dans le monde vivant.Allèle
: n.m Une des variantes possibles d'un gène *, s'exprimant dans le phénotype * d'une manière spécifique.Chromosome
: n.m Bâtonnet colorable se trouvant dans le noyau cellulaire, et dont la composante principale -l'ADN- contient, sous une forme codée l'information héréditaireCode génétique
: correspondance naturelle établie entre la séquence des nucléotides de l'ADN (ou celle l'ARN messager résultant de sa description) et la séquence spécdes aminoacides constituant les protèinesGène
: n.m Les facteurs héréditaires -révélés par les lois de MENDEL-Génétique évolutive des populations
: n.f s'occupe de la dynamique de la fréquence des gènes dans le cadre de population biologique.Génome
: n.m 1. La totalité du matériel héréditaire ; 2. Le patrimoine génétique d'un organisme donné. (Comparer avec génotype.)Génotype
: n.m La totalité des informations héréditaires virtuelles contenus dans le génome* et dont une partie, constituée par les caractères dominants, peut s'exprimer dans le phénotype.Haploïde
: adj. Se dit d'une cellule possédant une garniture simple de n chromosomes dans son génome. C'est notamment le cas des cellules sexuelles.Mutation
: n.f Variation héréditaire accidentelle causée par une modification du programme génétique porté par une molécule d'ADN. Selon l'ampleur des conséquences qu 'elle engendre.Phénotype
: n.m La totalité des caractères anatomiques, morphologiques, physiologiques éthologiques caractérisant un être vivant donné. Le phénotype représente la réalisation du génotype en fonction de certaines conditions du milieu.Sélection naturelle
: n.f Charles Darwin et alfred R.Wallace (1823-1913), indépendamment l'un de l'autre, ont constaté le rôle essentiel de la sélection naturelle dans l'évolution des espèces. Mais c'est le grand mérite de darwin que d'avoir fait la sélection naturelle le noyau durable de sa théorie d'évolution.![]()
Références
-1- Genetic Algorithm. Proeedings of the 7symposium on Multidisciplinary Optimisation. .
-2- Trusses by Genetic algorithms. ASME Winter Meeting.
-3- GOLDBERG, D.E .,1989, Genitic Algorithms in search, Optimisation and Machine
Learning, Addison Wesley
-4- Buckling laod Maximization by genetic algorithm. AIAA journal, Vol.31N°5,pp951-957.
-5- Samy.Missoum @ema.fr
-6- Dictionnaire de biologie DENIS BUICAN larousse-bordas 1997